题目内容
已知函数f(x)=ex-bx.
(Ⅰ) 若曲线y=f(x)在点(0,f(0))处的切线平行于x轴,求实数b的值;
(Ⅱ)若?x∈(0,+∞),f(x)≥0成立,求实数b的取值范围;
(Ⅲ)求证:
+
+…+
>n-ln(n+1)(n∈N*).
(Ⅰ) 若曲线y=f(x)在点(0,f(0))处的切线平行于x轴,求实数b的值;
(Ⅱ)若?x∈(0,+∞),f(x)≥0成立,求实数b的取值范围;
(Ⅲ)求证:
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)利用导函数在x=0处的值等于零,可以求出b的值.
(Ⅱ)在x>0时,函数的最小值大于等于0,求出b的值;
(Ⅲ)在(Ⅱ)的前提下,取b的一个特殊值为e时,再利用(Ⅱ)的结论,利用累加法即可证明不等式.
(Ⅱ)在x>0时,函数的最小值大于等于0,求出b的值;
(Ⅲ)在(Ⅱ)的前提下,取b的一个特殊值为e时,再利用(Ⅱ)的结论,利用累加法即可证明不等式.
解答:
解:(Ⅰ) f(x)=ex-bx,f'(x)=ex-b,
∵曲线y=f(x)在点(0,f(0))处的切线平行于x轴,∴f′(0)=0,即1-b=0,∴b=1.
(Ⅱ)依题意得,不等式ex-bx≥0即b≤
在(0,+∞)恒成立,
设g(x)=
(x>0),则g′(x)=
,
当x∈(0,1)时,g'(x)<0;当x∈(1,+∞)时,g'(x)>0,
∴函数g(x)在(0,1)单调递减,在(1,+∞)单调递增,
∴x∈(0,+∞),g(x)min=g(1)=e,∴b≤e.
∴实数b的取值范围为(-∞,e].
(Ⅲ)由(Ⅱ)知,当b=e时,?x∈(0,+∞),f(x)=ex-ex≥0
(当且仅当x=1时等号成立)∴x∈(0,+∞),ex≥ex,∴lnex≥lnex,即x≥1+lnx,(当且仅当x=1时等号成立),
设x=
,(n∈N*),则
>1+ln
,
∴
+
+…+
>(1+ln
)+(1+ln
)+…+(1+ln
),
又(1+ln
)+(1+ln
)+…+(1+ln
)=n+ln(
•
•…•
)=n+ln
=n-ln(n+1)
∴
+
+…+
>n-ln(n+1).
∵曲线y=f(x)在点(0,f(0))处的切线平行于x轴,∴f′(0)=0,即1-b=0,∴b=1.
(Ⅱ)依题意得,不等式ex-bx≥0即b≤
| ex |
| x |
设g(x)=
| ex |
| x |
| ex(x-1) |
| x2 |
当x∈(0,1)时,g'(x)<0;当x∈(1,+∞)时,g'(x)>0,
∴函数g(x)在(0,1)单调递减,在(1,+∞)单调递增,
∴x∈(0,+∞),g(x)min=g(1)=e,∴b≤e.
∴实数b的取值范围为(-∞,e].
(Ⅲ)由(Ⅱ)知,当b=e时,?x∈(0,+∞),f(x)=ex-ex≥0
(当且仅当x=1时等号成立)∴x∈(0,+∞),ex≥ex,∴lnex≥lnex,即x≥1+lnx,(当且仅当x=1时等号成立),
设x=
| n |
| n+1 |
| n |
| n+1 |
| n |
| n+1 |
∴
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
又(1+ln
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
| 1 |
| n+1 |
∴
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
点评:本题主要考查函数、导数、不等式等基本知识;考查运算求解能力、推理论证能力;考查化归转化思想、函数方程的思想、分类整合思想,累加法求和.属于难题.

练习册系列答案
相关题目
已知实数x,y满足不等式组
,则目标函数z=3x-4y的最小值m与最大值M的积为( )
|
| A、-60 | B、-48 |
| C、-80 | D、36 |
设正项等比数列{an}的前n项和为Sn,公比为q,若Sk-2=3,Sk=15,Sk+2=63,则q=( )
| A、-2 | B、2 | C、-4 | D、4 |
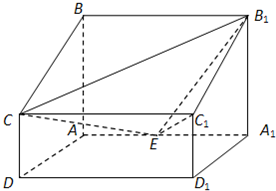 四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为AA1的中点.
四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB∥CD,AB⊥AD,AD=CD=1,AA1=AB=2,E为AA1的中点.