题目内容
17.设函数$f(x)=\frac{{3{x^2}+ax}}{e^x}({a∈R})$.若f(x)在x=0处取得极值,求曲线y=f(x)在点(1,f(1))处的切线方程为y=$\frac{3}{e}$x.分析 求出导数,可得f'(0)=0,解出a=0,可得切线斜率和切点,运用点斜式方程可得切线方程.
解答 解:函数$f(x)=\frac{{3{x^2}+ax}}{e^x}({a∈R})$的导数为$f'(x)=\frac{{-3{x^2}+(6-a)x+a}}{e^x}$,
由条件知f'(0)=0得a=0,
则$f(x)=\frac{{3{x^2}}}{e^x},f'(x)=\frac{{-3{x^2}+6x}}{e^x},f(1)=\frac{3}{e},f'(1)=\frac{3}{e}$,
则曲线y=f(x)在点(1,f(1))处的切线方程为$y-\frac{3}{e}=\frac{3}{e}(x-1)$,
即$y=\frac{3}{e}x$.
故答案为:y=$\frac{3}{e}$x.
点评 本题考查导数的运用:求切线方程和极值点,考查导数的几何意义,正确求导和运用点斜式方程是解题关键,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
2.已知一个几何体的三视图如图所示,则该几何体的体积为( )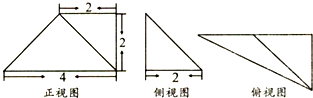

| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
6.已知几何体的三视图如图所示,则该几何体的体积为( )
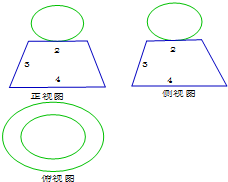

| A. | $\frac{π}{3}(4+14\sqrt{2})$ | B. | $\frac{{14\sqrt{2}π}}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{4π}{3}$ |
 如图,三棱锥的四个顶点P、A、B、C在同一个球面上,顶点P在平面ABC内的射影是H,若球心在直线PH上,则点H一定是△ABC的( )
如图,三棱锥的四个顶点P、A、B、C在同一个球面上,顶点P在平面ABC内的射影是H,若球心在直线PH上,则点H一定是△ABC的( )