题目内容
5.在直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=2-\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数).在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ.(Ⅰ) 求圆C的直角坐标方程;并判断直线l与圆C的位置关系.
(Ⅱ) 设圆C与直线l交于点A、B,若点P的坐标为(2,1),求|PA|+|PB|
分析 (1))直线l的参数方程化为普通方程,得:x+y-3=0,把圆C的方程为ρ=4cosθ化为普通方程,得:x2+y2=4x,求出圆心到直线距离,即可得到结论;
(Ⅱ)利用P(2,1)在弦AB上,根据直线的参数方程是几何意义可得结论.
解答 解:(Ⅰ)直线l的参数方程$\left\{\begin{array}{l}{x=2-\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数).
化为普通方程,得:x+y-3=0…..3分
把圆C的方程为ρ=4cosθ化为普通方程,得:x2+y2=4x…..6分
即(x-2)2+y2=4
点C到l的距离d=$\frac{|2+0-3|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$<2,
∴直线l与圆C相交.
(Ⅱ)设点A,B对应的参数分别为t1,t2,将$\left\{\begin{array}{l}{x=2-\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数).
带入(x-2)2+y2=4整理得:${t}^{2}+\sqrt{2}t-3=0$,
则$\left\{\begin{array}{l}{{t}_{1}+{t}_{2}=-\sqrt{2}}\\{{t}_{1}{t}_{2}=-3}\end{array}\right.$
又|PA|+|PB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{14}$.
点评 本题考查了极坐标化为直角坐标方程的方法、直线与圆相交问题,考查了推理能力与计算能力,属于中档题

 同步练习强化拓展系列答案
同步练习强化拓展系列答案
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
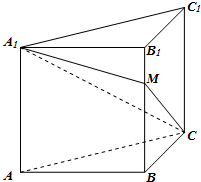 正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.
正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.