题目内容
5.向如图所示的矩形区域内随机投100个点,阴影面积为以下程序框图中的输出的s,当输入的n=10000时,请估算落在阴影区域内的点的个数 (结果四舍五入)为( )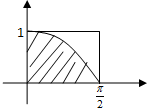

| A. | 60 | B. | 62 | C. | 64 | D. | 66 |
分析 分别求出矩形区域的面积和阴影部分的面积,代入几何概型概率计算公式,即可得到答案.
解答 解:矩形区域的面积S=1×$\frac{π}{2}$=$\frac{π}{2}$,
阴影部分的面积为S阴影=${∫}_{0}^{\frac{π}{2}}$cosxdx=sinx|${\;}_{0}^{\frac{π}{2}}$=1,
由几何概型:$\frac{{S}_{阴影}}{{S}_{矩形面积}}$=$\frac{落在阴影区域的点数x}{100}$,可得:$\frac{1}{\frac{π}{2}}$=$\frac{x}{100}$,
解得:x=$\frac{200}{π}$=63.66≈64.
故选:C.
点评 本题考查的知识点是几何概型,其中利用积分公式,计算出阴影部分的面积是解答本题的关键.

练习册系列答案
相关题目
14.设抛物线y2=8x的焦点为F,P是抛物线上一点,若直线PF的倾斜角为120°,则|PF|=( )
| A. | $\frac{8}{3}$ | B. | 3 | C. | $\frac{8}{3}$或8 | D. | 3或8 |