��Ŀ����
��ȱ�����{an}������Ϊa1=2������Ϊq��qΪ����������������3a3��8a1��a5�ĵȲ��������{bn}����2n2-��t+bn��n+
bn=0��t��R��n��N*����
��1��������{an}��ͨ�ʽ��
��2����ȷ��t��ֵ��ʹ������{bn}Ϊ�Ȳ����У�
��3����{bn}Ϊ�Ȳ�����ʱ����ÿ��������k����ak��ak+1֮�����bk��2���õ�һ��������{cn}����Tn������{cn} ��ǰn��ͣ��Ƿ����m��ʹ��Tm=1180���������������m��ֵ���������ڣ���˵�����ɣ�
| 3 |
| 2 |
��1��������{an}��ͨ�ʽ��
��2����ȷ��t��ֵ��ʹ������{bn}Ϊ�Ȳ����У�
��3����{bn}Ϊ�Ȳ�����ʱ����ÿ��������k����ak��ak+1֮�����bk��2���õ�һ��������{cn}����Tn������{cn} ��ǰn��ͣ��Ƿ����m��ʹ��Tm=1180���������������m��ֵ���������ڣ���˵�����ɣ�
���㣺�����벻��ʽ���ۺ�,���е�Ӧ��,�ȱ����е�����
ר�⣺�Ȳ�������ȱ�����
��������1��������֪����������ȣ�Ȼ��������{an}��ͨ�ʽ��
��2��������֪�������bn�ı���ʽ������{bn}Ϊ�Ȳ����У��������t��ֵ��
��3���������������{bn}�У�am����ǰ��������֮�ͣ�Ȼ�����a9��1180��a10���������a10������{bn}�е��������������m��ֵ��
��2��������֪�������bn�ı���ʽ������{bn}Ϊ�Ȳ����У��������t��ֵ��
��3���������������{bn}�У�am����ǰ��������֮�ͣ�Ȼ�����a9��1180��a10���������a10������{bn}�е��������������m��ֵ��
���
�⣺��1����ȱ�����{an}������Ϊa1=2������Ϊq��qΪ����������������3a3��8a1��a5�ĵȲ����
�ɵã�6a3=8a1+a5��6��2q2=8��2+2��q4�����q=2��
��an=2n��4��
��2������{bn}����2n2-��t+bn��n+
bn=0��t��R��n��N*����
��bn=
������b1=2t-4��b2=16-4t��b3=12-2t��
����b1+b3=2b2����t=3��8��
��t=3ʱ��bn=2n����bn-bn-1=2����������{bn}Ϊ�Ȳ����С�10��
��3������an=2n
��������{bn}��ak=2k��ak+1=2k+1��
��ÿ��������k����ak��ak+1֮�����bk��2���ɵ�һ��������{cn}����Tn������{cn} ��ǰn��ͣ�
������{bn}�У�am����ǰ��������֮��Ϊ[2+22+��+2m-1+2m]+��2��2+2��4+��+4m��=2m2+2m+1+
2m��
��2��92+29+2��9=692��1180��2��102+210+2��10=1244����a9��1180��a10��
����m��ʹ��Tm=1180��
����m=9+��b1+b2+��+b8��+8=9+2+4+6+8+10+14+16+8=89 ��16�֣�
�ɵã�6a3=8a1+a5��6��2q2=8��2+2��q4�����q=2��
��an=2n��4��
��2������{bn}����2n2-��t+bn��n+
| 3 |
| 2 |
��bn=
| 2n2-tn | ||
n-
|
����b1+b3=2b2����t=3��8��
��t=3ʱ��bn=2n����bn-bn-1=2����������{bn}Ϊ�Ȳ����С�10��
��3������an=2n
��������{bn}��ak=2k��ak+1=2k+1��
��ÿ��������k����ak��ak+1֮�����bk��2���ɵ�һ��������{cn}����Tn������{cn} ��ǰn��ͣ�
������{bn}�У�am����ǰ��������֮��Ϊ[2+22+��+2m-1+2m]+��2��2+2��4+��+4m��=2m2+2m+1+
2m��
��2��92+29+2��9=692��1180��2��102+210+2��10=1244����a9��1180��a10��
����m��ʹ��Tm=1180��
����m=9+��b1+b2+��+b8��+8=9+2+4+6+8+10+14+16+8=89 ��16�֣�
���������⿼���˵Ȳ����е�ͨ�ʽ�Լ������벻��ʽ���ۺϣ��ۺ���ǿ���ѶȽϴ��ڲ���ʽ���������ͨ��ת���ɺ�����ֵ�����������

��ϰ��ϵ�д�
 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�
�����Ŀ
P��˫����
-
=1��һ�㣬F1��F2��˫���ߵ��������㣬��|PF1|=17����|PF2|��ֵΪ��������
| x2 |
| 64 |
| y2 |
| 36 |
| A��33 | B��33��1 |
| C��1 | D��25��9 |
������x2=
y���߷�����y-2=0����a��ֵ�ǣ�������
| 1 |
| a |
A��
| ||
B��-
| ||
| C��8 | ||
| D��-8 |
�ڡ�ABC�У���֪a=4��b=4
��A=30�㣬BΪ��ǣ���ô��A��B��C�Ĵ�С��ϵΪ��������
| 3 |
| A��A��B��C |
| B��B��A��C |
| C��C��B��A |
| D��C��A��B |
 ����ǡ�ABC�У�BC=5��sinA=
����ǡ�ABC�У�BC=5��sinA=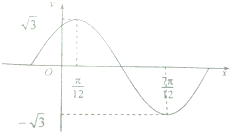 ��֪����f��x��=Asin����x+�գ���A��0���أ�0��0���գ�
��֪����f��x��=Asin����x+�գ���A��0���أ�0��0���գ�