题目内容
5.已知过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F(-c,0)和虚轴端点E的直线交双曲线的右支于点P,若E为线段FP的中点,则该双曲线的离心率为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\sqrt{5}$+1 |
分析 由题意,P(c,2b),代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{{c}^{2}}{{a}^{2}}-\frac{4{b}^{2}}{{b}^{2}}$=1,即可求出该双曲线的离心率.
解答 解:由题意,P(c,2b),代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{{c}^{2}}{{a}^{2}}-\frac{4{b}^{2}}{{b}^{2}}$=1,
∴e=$\sqrt{5}$,
故选B.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
16.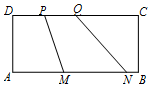 如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )
如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )
 如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )
如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
20.等差败列{an}的前n项和为Sn,若a3+a16=10,则S18=( )
| A. | 50 | B. | 90 | C. | 100 | D. | 190 |
17.如果直线l1:x+ax+1=0和直线l2:ax+y+1=0垂直,则实数a的值为( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 0 |
14.椭圆$\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{11}$=1的焦点坐标为( )
| A. | (±3$\sqrt{2}$,0) | B. | (±2,0) | C. | (0,±3$\sqrt{2}$) | D. | (0,±2) |
15.不等式3+5x-2x2>0的解集为( )
| A. | (-3,$\frac{1}{2}$) | B. | (-∞,-3)∪($\frac{1}{2}$,+∞) | C. | (-$\frac{1}{2}$,3) | D. | (-∞,-$\frac{1}{2}$)∪(3,+∞) |
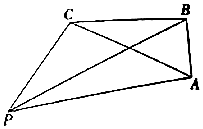 如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.
如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.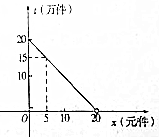 2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价-供货价格)
2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价-供货价格)