题目内容
14.某中学有学生270人,其中一年级108人,二、三年级各81人,现要用抽样方法抽取10人组成一个样本.将学生按一、二、三年级依次同一编号为1,2,…,270.如果抽得号码有如下四种情况:①5,9,100,107,111,121,180,195,200,265;
②7,34,61,88,115,142,169,196,223,250;
③30,57,84,111,138,165,192,219,246,270;
④11,38,60,90,119,146,173,200,227,254.
则其中可能由分层抽样、而不可能由系统抽样得到的样本是( )
| A. | ①② | B. | ①④ | C. | ②③ | D. | ②④ |
分析 先考虑那种情况为分层抽样,根据分层抽样的概念,需把总体按个体差异分成几层,再按每层的比抽取样本.
然后,再几种分层抽样中,再考虑哪几种是系统抽样,在系统抽样中,要抽取的样本容量是几,需把总体分成几部分,再按事先约定好的方法再每部分中抽取1个个体,就得到了样本.
解答 解:先考虑那种情况为分层抽样,分层抽样需按年级分成三层,一年级抽4个人,二三年级个抽3个人,也即1到108号抽4个,109到189号抽3个,190到270号抽3个,可判断①②④是分层抽样,
在判断①②④中那几个是系统抽样,系统抽样需把1到270号分成均与的10部分,每部分按事先约定好的方法抽取1个,则②为系统抽样.
故选B
点评 本题考查了抽样方法中,分层抽样和系统抽样,做题时应看清题意,避免不必要的错误.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
5.某四棱锥的三视图如图所示,该四棱锥的表面积是( )


| A. | 32 | B. | 16+16$\sqrt{2}$ | C. | 48 | D. | 16+32$\sqrt{2}$ |
9.函数f(x)=sin(2x+$\frac{π}{3}$)( )
| A. | 图象向右平移$\frac{π}{3}$个单位长度得到y=sin2x图象 | |
| B. | 图象关于点($\frac{π}{6}$,0)对称 | |
| C. | 图象关于直线x=-$\frac{π}{12}$对称 | |
| D. | 在区间[-$\frac{5π}{12}$,$\frac{π}{12}$]单调递增 |
16.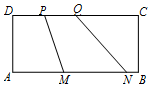 如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )
如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )
 如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )
如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
 某公司13个部门接受的快递的数量如茎叶图所示,则这13个部门接受的快递的数量的中位数为10.
某公司13个部门接受的快递的数量如茎叶图所示,则这13个部门接受的快递的数量的中位数为10.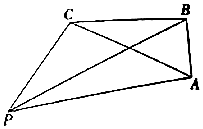 如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.
如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.