题目内容
13.在直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}x=1+tcosα\\ y=2+tsinα\end{array}\right.(t$为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴非负半轴为极轴)中,圆C的方程为ρ=6sinθ(1)求圆C的直角坐标方程;
(2)若点P(1,2),设圆C与直线l交于点A、B,求$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}$的最小值.
分析 (1)利用极坐标与直角坐标的互化方法,求圆C的直角坐标方程;
(2)利用参数的几何意义,求$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}$的最小值.
解答 解:(1)圆C的方程为ρ=6sinθ,可化为直角坐标方程为x2+y2=6y,即x2+(y-3)2=9;
(2)直线l的参数方程为$\left\{\begin{array}{l}x=1+tcosα\\ y=2+tsinα\end{array}\right.(t$为参数),代入x2+(y-3)2=9,可得t2+2(cosα-sinα)t-7=0,
∴t1+t2=-2(cosα-sinα),t1t2=-7,
∴$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}$=$\frac{|{t}_{1}-{t}_{2}|}{|{t}_{1}{t}_{2}|}$=$\frac{1}{7}\sqrt{4(cosα-sinα)^{2}+28}$=$\frac{1}{7}\sqrt{32-4sin2α}$≥$\frac{2\sqrt{7}}{7}$,
∴$\frac{1}{{|{PA}|}}+\frac{1}{{|{PB}|}}$的最小值为$\frac{2\sqrt{7}}{7}$.
点评 本题考查极坐标与直角坐标的互化,考查参数方程的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.某四棱锥的三视图如图所示,该四棱锥的表面积是( )


| A. | 32 | B. | 16+16$\sqrt{2}$ | C. | 48 | D. | 16+32$\sqrt{2}$ |
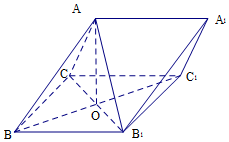 如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C 为菱形,B1C与BC1交于点O,AO⊥平面BB1C1C
如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C 为菱形,B1C与BC1交于点O,AO⊥平面BB1C1C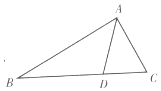 如图,在△ABC中,$AB=2AC,cosB=\frac{{2\sqrt{5}}}{5}$,点D在线段BC上.
如图,在△ABC中,$AB=2AC,cosB=\frac{{2\sqrt{5}}}{5}$,点D在线段BC上.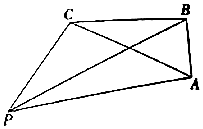 如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.
如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.