题目内容
设函数f(x)=x3-2x
(1)求函数的单调区间;
(2)若过点(1,a)可作三条直线与曲线y=f(x)相切,求a范围.
(1)求函数的单调区间;
(2)若过点(1,a)可作三条直线与曲线y=f(x)相切,求a范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)先求出f′(x)=3x2-2,令f′(x)>0,令f′(x)<0,解不等式,从而f(x)在(-∞,-
),(
,+∞)递增,在(-
,
)递减;
(2))因f′(x)=3x2-2,设切点(k,k3-2k),从而斜率K=3k2-2,求出a=-2k3+3k2-2,只需满足y=a和y=-2k3+3k2-2有3个解得即可,画出函数y=-2k3+3k2-2的图象,一目了然.
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
(2))因f′(x)=3x2-2,设切点(k,k3-2k),从而斜率K=3k2-2,求出a=-2k3+3k2-2,只需满足y=a和y=-2k3+3k2-2有3个解得即可,画出函数y=-2k3+3k2-2的图象,一目了然.
解答:
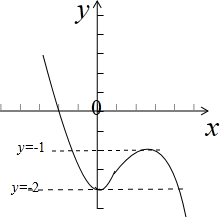 解:(1)∵f′(x)=3x2-2,
解:(1)∵f′(x)=3x2-2,
令f′(x)>0,解得:x>
,或x<-
,
令f′(x)<0,解得:-
<x<
;
∴f(x)在(-∞,-
),(
,+∞)递增,在(-
,
)递减;
(2))∵f′(x)=3x2-2,设切点(k,k3-2k),
∴斜率K=3k2-2,
∴a=-2k3+3k2-2,
∴只需满足y=a和y=-2k3+3k2-2有3个解得即可,
画出函数y=-2k3+3k2-2的图象,
如图示:
∴-2<a<-1.
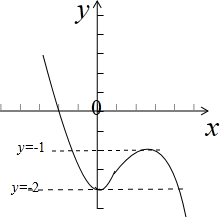 解:(1)∵f′(x)=3x2-2,
解:(1)∵f′(x)=3x2-2,令f′(x)>0,解得:x>
| ||
| 3 |
| ||
| 3 |
令f′(x)<0,解得:-
| ||
| 3 |
| ||
| 3 |
∴f(x)在(-∞,-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
(2))∵f′(x)=3x2-2,设切点(k,k3-2k),
∴斜率K=3k2-2,
∴a=-2k3+3k2-2,
∴只需满足y=a和y=-2k3+3k2-2有3个解得即可,
画出函数y=-2k3+3k2-2的图象,
如图示:
∴-2<a<-1.
点评:本题考察了函数的单调性,导数的应用,渗透数形结合思想,转化思想,是一道综合题.

练习册系列答案
相关题目
高二年级6个班进行单循环篮球比赛(每两个班比赛一场),则比赛的总场次数是( )
A、A
| ||||||
B、A
| ||||||
C、C
| ||||||
D、C
|
已知函数y=
+
的最大值为M,最小值为m,则
的值为( )
| 1-x |
| x+5 |
| M |
| m |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
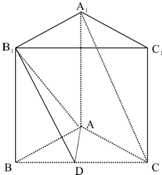 如图,正三棱柱ABC-A1B1C1中,D是BC中点,AA1=AB=a.
如图,正三棱柱ABC-A1B1C1中,D是BC中点,AA1=AB=a.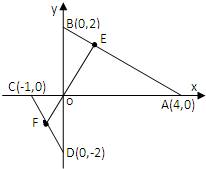 在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.
在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线. 一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形.
一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形.