题目内容
设函数f（x）=x2+
+alnx，a∈R，其导函数为f′（x）；
（Ⅰ）当a=-4时，求f（x）的单调区间；
（Ⅱ）当a≤4时，?x1，x2∈（0，+∞），x1≠x2，求证：|f′（x1）-f′（x2）|＞|x1-x2|．
| 2 |
| x |
（Ⅰ）当a=-4时，求f（x）的单调区间；
（Ⅱ）当a≤4时，?x1，x2∈（0，+∞），x1≠x2，求证：|f′（x1）-f′（x2）|＞|x1-x2|．
考点：利用导数研究函数的单调性,绝对值不等式的解法
专题：导数的综合应用
分析：（1）当a=-4时，f′（x）=
，（x＞0），令f′（x）≥0，令f′（x）＜0，从而函数f（x）的单调增区间为[
，+∞）单调减区间为（0，
），
（2）f′（x）=2x-
+
，得|2+
-
|＞1，从而有2+
-
＞1恒成立，只需证明：x1 x2+
≥a即可，对此：设t=
，t＞0，u（t）=t2+
，而u（t）=t2+
+
≥3
=
＞4≥a，故命题得证．
| 2(x3-2x-1) |
| x2 |
1+
| ||
| 2 |
1+
| ||
| 2 |
（2）f′（x）=2x-
| 2 |
| x2 |
| a |
| x |
| 2(x1+x2) |
| x12x22 |
| a |
| x2x1 |
| 2(x1+x2) |
| x12x22 |
| a |
| x2x1 |
| 4 | ||
|
| x1x2 |
| 4 |
| t |
| 2 |
| t |
| 2 |
| t |
| 3 | 4 |
| 3 | 108 |
解答：
解：（1）当a=-4时，f′（x）=
，（x＞0），
令f′（x）≥0，即：x3-2x-1≥0，（x+1）（x2-x-1）≥0，解得：x≥
，
令f′（x）＜0，解得：0＜x＜
，
∴函数f（x）的单调增区间为[
，+∞）单调减区间为（0，
），
（2）f′（x）=2x-
+
，
∴|f′（x1 ）-f′（x2 ）|=|x1-x2||2+
-
|，
∴|2+
-
|＞1
下面证明?x1，x2∈（0，+∞），x1≠x2，
有2+
-
＞1恒成立，
即证：a＜x1x2+
成立，
∵x1x2+
＞x1 x2+
，
∴只需证明：x1 x2+
≥a即可，
对此：设t=
，t＞0，u（t）=t2+
，
而u（t）=t2+
+
≥3
=
＞4≥a，
∴即证：a＜x1x2+
成立，
∴a＜x1x2+
．
故命题得证．
| 2(x3-2x-1) |
| x2 |
令f′（x）≥0，即：x3-2x-1≥0，（x+1）（x2-x-1）≥0，解得：x≥
1+
| ||
| 2 |
令f′（x）＜0，解得：0＜x＜
1+
| ||
| 2 |
∴函数f（x）的单调增区间为[
1+
| ||
| 2 |
1+
| ||
| 2 |
（2）f′（x）=2x-
| 2 |
| x2 |
| a |
| x |
∴|f′（x1 ）-f′（x2 ）|=|x1-x2||2+
| 2(x1+x2) |
| x12x22 |
| a |
| x2x1 |
∴|2+
| 2(x1+x2) |
| x12x22 |
| a |
| x2x1 |
下面证明?x1，x2∈（0，+∞），x1≠x2，
有2+
| 2(x1+x2) |
| x12x22 |
| a |
| x2x1 |
即证：a＜x1x2+
| 2(x1+x2) |
| x1x2 |
∵x1x2+
| 2(x1+x2) |
| x1x2 |
| 4 | ||
|
∴只需证明：x1 x2+
| 4 | ||
|
对此：设t=
| x1x2 |
| 4 |
| t |
而u（t）=t2+
| 2 |
| t |
| 2 |
| t |
| 3 | 4 |
| 3 | 108 |
∴即证：a＜x1x2+
| 2(x1+x2) |
| x1x2 |
∴a＜x1x2+
| 2(x1+x2) |
| x1x2 |
故命题得证．
点评：本题考察了函数的单调性，导数的应用，不等式的证明，是一道综合题．
练习册系列答案
相关题目
已定义在R上的偶函数f（x）满足x∈（-∞，0）时，f（x）+xf′（x）＜0成立，若a=20.2f（20.2），b=ln2f（ln2），c=（log0.50.25）•f（log0.50.25），则a，b，c的大小关系是（ ）
| A、a＞b＞c |
| B、c＞a＞b |
| C、b＞a＞c |
| D、a＞c＞b |
已知向量
，
满足|
|=3，且|
+
|=|
-
|=5，则|
|=（ ）
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| b |
| A、4 | ||
| B、2 | ||
| C、8 | ||
D、
|
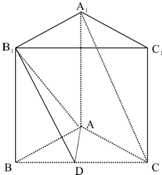如图，正三棱柱ABC-A1B1C1中，D是BC中点，AA1=AB=a．