题目内容
双曲线
-
=1上一点P到它一个焦点的距离是8，则P到另一个焦点的距离是（ ）
| x2 |
| 25 |
| y2 |
| 16 |
| A、18 | B、5 | C、2 | D、4 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：依题意，利用双曲线的概念||PF1|-|PF2||=10即可求得答案．
解答：
解：设双曲线
-
=1的左右焦点分别为F1，F2，则||PF1|-|PF2||=10，
双曲线双曲线
-
=1上一点P到一个焦点的距离为8，不妨令|PF2|=8，
则||PF1|-8|=10，
∴|PF1|=18．
故选：A．
| x2 |
| 25 |
| y2 |
| 16 |
双曲线双曲线
| x2 |
| 25 |
| y2 |
| 16 |
则||PF1|-8|=10，
∴|PF1|=18．
故选：A．
点评：本题考查双曲线的简单性质，着重考查双曲线的标准方程与定义的应用，属于中档题．
练习册系列答案
相关题目
如图，在以BC为直径的半圆上任取一点P，过弧BP的中点A作AD⊥BC于D．连接BP交AD于点E，交AC于点F，则BE：EF=（ ）| A、2：1 | B、1：1 |
| C、1：2 | D、以上结论都不对 |
高二年级6个班进行单循环篮球比赛（每两个班比赛一场），则比赛的总场次数是（ ）
A、A
| ||||||
B、A
| ||||||
C、C
| ||||||
D、C
|
正三棱锥底面边长为3，侧棱与底面成60°角，则正三棱锥外接球面积为（ ）
| A、4π | ||
B、4
| ||
| C、16π | ||
D、16
|
在△ABC中，角A，B，C的对边分别为a，b，c，若a2+b2=2014c2，则
+
=（ ）
| tanC |
| tanA |
| tanC |
| tanB |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
，
满足|
|=3，且|
+
|=|
-
|=5，则|
|=（ ）
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| b |
| A、4 | ||
| B、2 | ||
| C、8 | ||
D、
|
已知函数y=
+
的最大值为M，最小值为m，则
的值为（ ）
| 1-x |
| x+5 |
| M |
| m |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
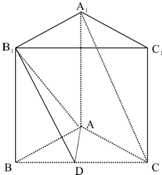如图，正三棱柱ABC-A1B1C1中，D是BC中点，AA1=AB=a．