题目内容
实数a、b、c满足a+b+c=0，abc＞0，则
+
+
的值（ ）
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| A、一定是正数 |
| B、一定是负数 |
| C、可能是0 |
| D、正、负不能确定 |
考点：不等关系与不等式
专题：不等式的解法及应用
分析：由条件可得 a、b、c中有2个是负数，有一个为正数．不妨设a＜0，b＜0，c＞0，且|a|＜|c|，利用不等式的基本性质可得
+
+
＜0．
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
解答：
解：根据a+b+c=0，abc＞0，可得 a、b、c中有2个是负数，有一个为正数．
不妨设a＜0，b＜0，c＞0，且|a|＜|c|，
∴
＞
，∴-
＞
．
而
＜0，∴
+
+
＜0，
故选：B．
不妨设a＜0，b＜0，c＞0，且|a|＜|c|，
∴
| 1 |
| |a| |
| 1 |
| |c| |
| 1 |
| a |
| 1 |
| c |
而
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
故选：B．
点评：本题考查了分式的计算和正数与负数的性质以及绝对值的含义，不等式的基本性质，属于基础题．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
等比数列的前10项和，前20项和，前30项的和分别为S，T，R，则（ ）
| A、S2+T2=S（T+R） |
| B、T2=SR |
| C、（S+T）-R=T2 |
| D、S+T=R |
如图，在以BC为直径的半圆上任取一点P，过弧BP的中点A作AD⊥BC于D．连接BP交AD于点E，交AC于点F，则BE：EF=（ ）| A、2：1 | B、1：1 |
| C、1：2 | D、以上结论都不对 |
命题“若∠C=90°，则△ABC是直角三角形”它的逆命题是（ ）命题．
| A、真 | B、假 | C、不确定 | D、D、 |
已知双曲线的标准方程为
-y2=1，则它的焦点坐标是（ ）
| x2 |
| 2 |
| A、（±1，0） | ||
B、（±
| ||
C、（0，±
| ||
| D、（0，±1） |
已定义在R上的偶函数f（x）满足x∈（-∞，0）时，f（x）+xf′（x）＜0成立，若a=20.2f（20.2），b=ln2f（ln2），c=（log0.50.25）•f（log0.50.25），则a，b，c的大小关系是（ ）
| A、a＞b＞c |
| B、c＞a＞b |
| C、b＞a＞c |
| D、a＞c＞b |
高二年级6个班进行单循环篮球比赛（每两个班比赛一场），则比赛的总场次数是（ ）
A、A
| ||||||
B、A
| ||||||
C、C
| ||||||
D、C
|
正三棱锥底面边长为3，侧棱与底面成60°角，则正三棱锥外接球面积为（ ）
| A、4π | ||
B、4
| ||
| C、16π | ||
D、16
|
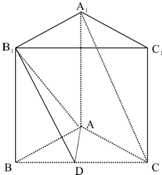如图，正三棱柱ABC-A1B1C1中，D是BC中点，AA1=AB=a．