题目内容
已知函数f(x)=ax2+
+5(常数a,b∈R)满足f(1)+f(-1)=14.
(1)求出a的值,并就常数b的不同取值讨论函数f(x)奇偶性;
(2)若f(x)在区间(-∞,-
)上单调递减,求b的最小值;
(3)在(2)的条件下,当b取最小值时,证明:f(x)恰有一个零点q且存在递增的正整数数列{an},使得
=q a1+q a2+q a3+…+q an+…成立.
| b |
| x |
(1)求出a的值,并就常数b的不同取值讨论函数f(x)奇偶性;
(2)若f(x)在区间(-∞,-
| 3 | 0.5 |
(3)在(2)的条件下,当b取最小值时,证明:f(x)恰有一个零点q且存在递增的正整数数列{an},使得
| 2 |
| 5 |
考点:利用导数研究函数的单调性,函数奇偶性的判断
专题:函数的性质及应用,导数的概念及应用,等差数列与等比数列
分析:(1)根据条件很容易求出a,讨论奇偶性根据定义即可,注意对于非奇非偶的,要举出反例.
(2)利用导数求出f(x)的单调区间,再与所给单调区间比较即可求b的最小值.
(3)说f(x)有一个零点,所以我们先来找f(x)的零点,找到之后再看怎样让它满足所给等式即可.
(2)利用导数求出f(x)的单调区间,再与所给单调区间比较即可求b的最小值.
(3)说f(x)有一个零点,所以我们先来找f(x)的零点,找到之后再看怎样让它满足所给等式即可.
解答:
解:(1)由f(1)+f(-1)=14得(a+b+5)+(a-b+5)=14,所以解得a=2;
所以f(x)=2x2+
+5,定义域为(-∞,0)∪(0,+∞);
当b=0时,对于定义域内的任意x,有f(-x)=f(x)=2x2+5,所以f(x)为偶函数.
当b≠0时,f(1)+f(-1)=14≠0,所以f(-1)≠-f(1),所以f(x)不是奇函数;f(-1)-f(1)=-2b≠0,所以f(x)不是偶函数;
所以,b=0时f(x)为偶函数,b≠0时,f(x)为非奇非偶函数.
(2)f′(x)=4x-
=
=0,解得x=
,所以x∈(-∞,
)时,f′(x)<0,所以f(x)在(-∞,
)上单调递减,又f(x)在(-∞,-
)上单调递减,所以-
≤
,解得 b≥-2,所以b的最小值是-2.
(3)在(2)的条件下,f(x)=2x2-
+5;
当 x<0时,f(x)>0恒成立,函数f(x)在(-∞,0)上无零点;
当 x>0时,f′(x)=4x+
>0,所以函数f(x)在(0,+∞)上递增,又f(
)=-
<0,f(1)=5>0;
∴f(x)在(
,1)上有一个零点q,即q∈(
,1),且f(q)=2q2-
+5=0,整理成
=
,所以
=
;
又
=q+q4+q7+…+q3n-2++…,所以
=q+q4+q7+…+q3n-2+…,且an=3n-2.
所以f(x)=2x2+
| b |
| x |
当b=0时,对于定义域内的任意x,有f(-x)=f(x)=2x2+5,所以f(x)为偶函数.
当b≠0时,f(1)+f(-1)=14≠0,所以f(-1)≠-f(1),所以f(x)不是奇函数;f(-1)-f(1)=-2b≠0,所以f(x)不是偶函数;
所以,b=0时f(x)为偶函数,b≠0时,f(x)为非奇非偶函数.
(2)f′(x)=4x-
| b |
| x2 |
| 4x3-b |
| x2 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 | 0.5 |
| 3 | 0.5 |
| 3 |
| ||
(3)在(2)的条件下,f(x)=2x2-
| 2 |
| x |
当 x<0时,f(x)>0恒成立,函数f(x)在(-∞,0)上无零点;
当 x>0时,f′(x)=4x+
| 2 |
| x2 |
| 1 |
| 4 |
| 23 |
| 8 |
∴f(x)在(
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| q |
| 1-q3 |
| q |
| 5 |
| 2 |
| q |
| 1-q3 |
| 2 |
| 5 |
又
| q |
| 1-q3 |
| 2 |
| 5 |
点评:本题前两问比较基础,只是在第二问中注意,要说明一个函数非奇非偶,只需举出反例即可.对于第三问,你要去寻找零点,寻找的最后找到了零点所在的区间,零点,即函数在零点处取值为零,所以会得到关于q的一个等式,经过变形就出来了所给等式中的
,得到等式
=
之后,会看出
很像某个等比数列的和,从而完成了本题的求解.
| 2 |
| 5 |
| q |
| 1-q3 |
| 2 |
| 5 |
| q |
| 1-q3 |

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
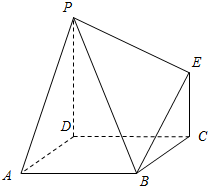 如图,简单组合体ABCDPE,其底面ABCD是边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.
如图,简单组合体ABCDPE,其底面ABCD是边长为2的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=2. 在直角梯形中ABCD中.AB∥CD,AB⊥BC,F为AB上的点,且BE=1,AD=AE=DC=2,将△ADE沿DE折叠到P点,使PC=PB.
在直角梯形中ABCD中.AB∥CD,AB⊥BC,F为AB上的点,且BE=1,AD=AE=DC=2,将△ADE沿DE折叠到P点,使PC=PB.