题目内容
已知函数f(x)=
x3-x2
(1)求f(x)在R上的极值;
(2)已知a∈R,若g(x)=f(x)+ax,讨论g(x)的单调性.
| 1 |
| 3 |
(1)求f(x)在R上的极值;
(2)已知a∈R,若g(x)=f(x)+ax,讨论g(x)的单调性.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)先求出函数的导数,解不等式求出即可,(2)先求出函数g(x)的导数,分别讨论①a≥1时②a<1时的情况,从而求出单调区间.
解答:
解:(1)∵f′(x)=x(x-2),
令f′(x)>0,解得:x>2,或x<0,
令f′(x)<0,解得:0<x<2,
∴f(x)在(-∞,0),(2,+∞)递增,在(0,2)递减,
∴f(x)极大值=f(0)=0,f(x)极小值=f(2)=-
.
(2)∵g(x)=
x3-x2+ax,
∴g′(x)=x2-2x+a,
①a≥1时,g′(x)≥0,g(x)在(-∞,+∞)递增,
②a<1时,令g′(x)=0,解得:x=1±
,
∴f(x)在(-∞,1-
),(1+
,+∞)递增,在(1-
,1+
)递减.
令f′(x)>0,解得:x>2,或x<0,
令f′(x)<0,解得:0<x<2,
∴f(x)在(-∞,0),(2,+∞)递增,在(0,2)递减,
∴f(x)极大值=f(0)=0,f(x)极小值=f(2)=-
| 4 |
| 3 |
(2)∵g(x)=
| 1 |
| 3 |
∴g′(x)=x2-2x+a,
①a≥1时,g′(x)≥0,g(x)在(-∞,+∞)递增,
②a<1时,令g′(x)=0,解得:x=1±
| 1-a |
∴f(x)在(-∞,1-
| 1-a |
| 1-a |
| 1-a |
| 1-a |
点评:本题考察了函数的单调性,导数的应用,渗透了分类讨论思想,是一道综合题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
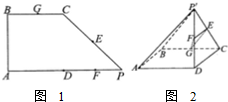 如图1所示,在直角梯形ABCP中,AP∥BC,AP⊥AB,AP=2AB=2BC,D是底边AP的中点,E.F、G分别为PC、PD、CB的中点,将△PCD沿CD折起,使点P位于点P′,且P′D⊥平面ABCD,得折叠后如图2的几何图形.
如图1所示,在直角梯形ABCP中,AP∥BC,AP⊥AB,AP=2AB=2BC,D是底边AP的中点,E.F、G分别为PC、PD、CB的中点,将△PCD沿CD折起,使点P位于点P′,且P′D⊥平面ABCD,得折叠后如图2的几何图形. 在长方体ABCD-A1B1C1D1中,已知AB=4,BC=3,CC1=5,求:
在长方体ABCD-A1B1C1D1中,已知AB=4,BC=3,CC1=5,求: