题目内容
已知实数x，y满足
时，z=
+
（a≥b＞0）的最大值为1，则a+b的最小值为 ．
|
| x |
| a |
| y |
| b |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，利用z=
+
（a≥b＞0）的最大值为1，得到a，b的关系，利用基本不等式即可得到结论．
| x |
| a |
| y |
| b |
解答：
解：作出不等式组对应的平面区域如图：
由z=
+
（a≥b＞0）得y=-
x+bz，
∵a≥b＞0，
∴直线斜率k=-
∈[-1，0），
平移直线y=-
x+bz，当直线y=-
x+bz经过点A时，y=-
x+bz的截距最大，此时z最大为1，
由
，解得
，即A（1，4），
此时
+
=1，
∴a+b=（a+b）（
+
）
=5+
+
≥5+2
=5+4=9，
当且仅当
=
即b=2a时取等号，
但此时不满足a≥b，
∴基本不等式不成立，
设t=
，∵a≥b＞0，∴0＜t≤1，
则g（t）=5+t+
在（0，1]上是单调递减的，
∴当t=1时，g（t）=5+t+
取得最小值g（1）=5+1+4=10
∴a+b的最小值为10，
故答案为：10．
由z=
| x |
| a |
| y |
| b |
| b |
| a |
∵a≥b＞0，
∴直线斜率k=-
| b |
| a |
平移直线y=-
| b |
| a |
| b |
| a |
| b |
| a |
由
|
|
此时
| 1 |
| a |
| 4 |
| b |
∴a+b=（a+b）（
| 1 |
| a |
| 4 |
| b |
=5+
| b |
| a |
| 4a |
| b |
|
当且仅当
| b |
| a |
| 4a |
| b |
但此时不满足a≥b，
∴基本不等式不成立，
设t=
| b |
| a |
则g（t）=5+t+
| 4 |
| t |
∴当t=1时，g（t）=5+t+
| 4 |
| t |
∴a+b的最小值为10，
故答案为：10．
点评：本题主要考查线性规划和基本不等式的应用，利用数形结合是解决本题的关键．当基本不等式不成立时，要使用函数f（x）=x+
，a＞0的单调性来解决．
| a |
| x |
练习册系列答案
金钥匙试卷系列答案
相关题目
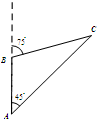一只艘船以均匀的速度由A点向正北方向航行，如图，开始航行时，从A点观测灯塔C的方位角（从正北方向顺时针转到目标方向的水平角）为45°，行驶60海里后，船在B点观测灯塔C的方位角为75°，则A到C的距离是