题目内容
已知sinαcosα=
,且α是第三象限角,求
-
的值.
| 1 |
| 8 |
| 1-cos2α |
| sinα-cosα |
| sinα+cosα |
| tan2α-1 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由条件求得 sinα+cosα 的值,再利用同角三角函数的基本关系化简要求的式子为sinα+cosα,从而得到答案.
解答:
解:已知sinαcosα=
,且α是第三象限角,∴sinα+cosα=-
=-
=-
.
-
=
-
=
-
=sinα+cosα=-
,
故答案为:-
.
| 1 |
| 8 |
| (sinα+cosα )2 |
| 1+2sinαcosα |
| ||
| 2 |
| 1-cos2α |
| sinα-cosα |
| sinα+cosα |
| tan2α-1 |
| sin2α |
| sinα-cosα |
| cos2α(sinα+cosα) |
| sin2α-cos2α |
| sin2α |
| sinα-cosα |
| cos2α |
| sinα-cosα |
| ||
| 2 |
故答案为:-
| ||
| 2 |
点评:本题主要考查同角三角函数的基本关系的应用,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
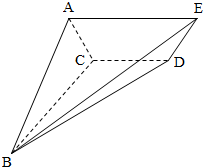 如图,四棱锥B-ACDE中,底面ACDE为直角梯形,CD∥AE,∠BCD=∠ACD=90°,二面角A-CD-B为60°,AE=BC=2,AC=CD=1.
如图,四棱锥B-ACDE中,底面ACDE为直角梯形,CD∥AE,∠BCD=∠ACD=90°,二面角A-CD-B为60°,AE=BC=2,AC=CD=1.