题目内容
若集合A={x|x>-2},B={x|bx>1},其中b为实数且b≠0,试写出:
(1)A∪B=R的一个充要条件;
(2)A∪B=R的一个必要非充分条件;
(3)A∪B=R的一个充分非必要条件.
(1)A∪B=R的一个充要条件;
(2)A∪B=R的一个必要非充分条件;
(3)A∪B=R的一个充分非必要条件.
考点:必要条件、充分条件与充要条件的判断
专题:集合,简易逻辑
分析:根据充分条件和必要条件的定义分别确定条件即可得到结论.
解答:
解:若b>0,则B={x|x>
},若b<0,则集合B={x|x<
}
(1)若A∪B=R,则必有
,即
,∴b<-
,
故A∪B=R的一个充要条件是b<-
.
(2)由(1)知A∪B=R充要条件是b<-
.
∴A∪B=R的一个必要非充分条件可以是b<0.
(3)由(1)知A∪B=R充要条件是b<-
.
∴A∪B=R的一个充分非必要条件b<-1
| 1 |
| b |
| 1 |
| b |
(1)若A∪B=R,则必有
|
|
| 1 |
| 2 |
故A∪B=R的一个充要条件是b<-
| 1 |
| 2 |
(2)由(1)知A∪B=R充要条件是b<-
| 1 |
| 2 |
∴A∪B=R的一个必要非充分条件可以是b<0.
(3)由(1)知A∪B=R充要条件是b<-
| 1 |
| 2 |
∴A∪B=R的一个充分非必要条件b<-1
点评:本题主要考查充分条件和必要条件的应用,根据定义是解决本题的关键,比较基础.

练习册系列答案
相关题目
设f(
)=x,则f′(x)=( )
| 1 |
| x |
| A、1 | ||
B、
| ||
C、-
| ||
| D、2x |
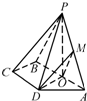 如图,已知四棱锥P-ABCD,底面ABCD是等腰梯形,且AB∥CD,O是AB中点,PO⊥平面ABCD,PO=CD=DA=
如图,已知四棱锥P-ABCD,底面ABCD是等腰梯形,且AB∥CD,O是AB中点,PO⊥平面ABCD,PO=CD=DA=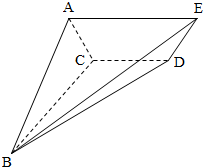 如图,四棱锥B-ACDE中,底面ACDE为直角梯形,CD∥AE,∠BCD=∠ACD=90°,二面角A-CD-B为60°,AE=BC=2,AC=CD=1.
如图,四棱锥B-ACDE中,底面ACDE为直角梯形,CD∥AE,∠BCD=∠ACD=90°,二面角A-CD-B为60°,AE=BC=2,AC=CD=1.