题目内容
化简并计算：
= ．
| cos83°+sin75°sin8° |
| cos7°-cos75°cos82° |
考点：运用诱导公式化简求值,同角三角函数基本关系的运用
专题：三角函数的求值
分析：原式中的角度变形后，利用诱导公式化简，再利用同角三角函数间基本关系变形，将tan75°的值代入计算即可求出值．
解答：
解：∵tan75°=tan（45°+30°）=
=
=2+
，
∴原式=
=
=
=
=
=2-
．
故答案为：2-
．
1+
| ||||
1-
|
12+6
| ||
| 6 |
| 3 |
∴原式=
| cos(75°+8°)+sin75°sin8° |
| cos(82°-75°)-cos75°cos82° |
| cos75°cos8° |
| sin82°sin75° |
| cos75°cos8° |
| cos8°sin75° |
| 1 |
| tan75° |
| 1 | ||
2+
|
| 3 |
故答案为：2-
| 3 |
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
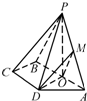如图，已知四棱锥P-ABCD，底面ABCD是等腰梯形，且AB∥CD，O是AB中点，PO⊥平面ABCD，PO=CD=DA=