题目内容

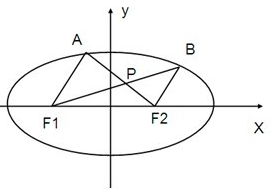在椭圆
x2
4
+y2=1中，F1、F2为椭圆的左右焦点，过F1和F2分别作直线F1A和F2B，使得F1A∥F2B，连接F2A和F1B，两直线交于点P，证明：PF1+PF2的定值．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：由已知条件推导出|PF1|+|PF2|=8-
2|AF1|•|BF2|
|AF1|+|BF2|
，再由F1(-
3
，0)，F2(
3
，0)，AF1∥BF2，推导出|AF1|+|BF2|=
4m2+4
m2+4
，|AF1|•|BF2|=
m2+1
m2+4
，由此能够证明|PF1|+|PF2|是定值．
解答： 证明：在椭圆
x2
4
+y2=1中，F1、F2为椭圆的左右焦点，
∵过F1和F2分别作直线F1A和F2B，使得F1A∥F2B，
∴
|PB|
|PF1|
=
|BF2|
|AF1|
，
∴
|PB|+|PF1|
|PF1|
=
|BF2|+|AF1|
|AF1|
，
∴|PF1|=
|AF1|
|AF1|+|BF2|
•|BF1|，
由B点在椭圆上，得到|BF1|+|BF2|=4，
∴|PF1|=
|AF1|
|AF1|+|BF2|
•|BF1|=
|AF1|
|AF1|+|BF2|
•（4-|BF2|），
同理|PF2|=
|AF1|
|AF1|+|BF2|
（4-|AF1|），
∴|PF1|+|PF2|=
|AF1|
|AF1|+|BF2|
•（4-|BF2|）+
|AF1|
|AF1|+|BF2|
（4-|AF1|）
=8-
2|AF1|•|BF2|
|AF1|+|BF2|
，
∵F1(-
3
，0)，F2(
3
，0)，AF1∥BF2，
∴设AF1：x+
3
=my，BF2：x-
3
=my，
设A（x1，y1），B（x2，y2），y1＞0，y2＞0，
由
x12
4
+y12=1
x1+
3
=my
，整理，得：
（m2+4)y12-2
3
my1-1=0，
∴y1=
3
m+2
m2+1
m2+4
，
∴AF1=
(x0+
3
)2+y12
=
(my1)2+y12
=
3(m2+1)
m+2m2+2
m2+4
，
同理，BF2=
-
3(m2+1)
m+2m2+2
m2+4
，
又由①②知|AF1|+|BF2|=
4m2+4
m2+4
，
|AF1|•|BF2|=
m2+1
m2+4

∴|PF1|+|PF2|=8-
2•
m2+1
m2+4
4m2+4
m2+4
=8-
1
2
=
7
2
．
∴|PF1|+|PF2|是定值．
点评：本题考查两数这和为定值的证明，解题时要认真审题，注意挖掘题设中的隐含条件，合理地进行等价转化．
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点分别为F1，F2，离心率为
2
2
，且过点(2，
2
)．
（1）求椭圆C的标准方程；
（2）过点F1作直线l1与椭圆交于M，N两点，过点F2作直线l2与椭圆交于P，Q两点，且直线l1，l2互相垂直，试问
1
|MN|
+
1
|PQ|
是否为定值？如果是，求出该定值；如果不是，求出其取值范围．
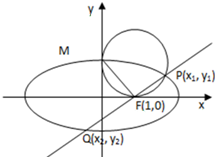椭圆G：
x2
a2
+
y2
b2
=1（a＞0，b＞0 ）与x轴交于A、B两点，F是它的右焦点，若
FA
•
FB
=-1且|OF|=1
（1）求椭圆C的标准方程；
（2）设椭圆G的上顶点为M，是否存在直线L，L交椭圆于P（x1，y1）、Q（x2，y2）两点，满足PQ⊥MF，且|PQ|=
4
3
，若存在，求直线L的方程，若不存在，请说明理由．
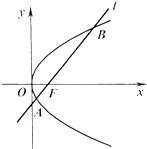如图，已知抛物线C：y2=4x焦点为F，直线l经过点F且与抛物线C相交于A，B两点
（Ⅰ）若线段AB的中点在直线y=1上，求直线l的方程；
（Ⅱ）若线段|AB|=20，求直线l的方程．
已知椭圆M：
x2
a2
+
y2
b2
=1（a＞b＞0）的一个顶点A的坐标是（0，-1），且右焦点Q到直线x-y+2
2
=0的距离为3．
（1）求椭圆方程；
（2）试问是否存在斜率为k（k≠0）的直线l，使l与椭圆M有两个不同的交点B、C，且|AB|=|AC|？若存在，求出k的范围，若不存在，说明理由．
若实数x，y满足
x-y+1≥0
x+y≥0
x≤0
，则目标函数z=x+2y的最大值是
 
．
若等边△ABC的边长为1，平面内一点M满足
CM
=
1
3
CB
+
1
2
CA
，则
MA
•
MB
=
 
．
给出下列命题：
①若A，B是锐角△ABC的两内角，则有sinA＞cosB；
②在同一坐标系中，函数y=sinx与y=lgx的交点个数为2个；
③如果
sinα-2cosα
3sinα+5cosα
=-5，那么tan α的值为-
23
16
；
④存在实数x，使得等式sinx+cosx=
3
2
成立；
⑤若0＜x≤1，则
sin2x
x2
＜
sinx
x

其中正确的命题为
 
（写出所有正确命题的序号）．
已知x，y满足
y-2≤0
x+3≥0
x-y-1≤0
，则
y+2
x-4
的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网