题目内容
已知离心率为
的椭圆C1的顶点A1,A2恰好是双曲线
-y2=1的左右焦点,点P是椭圆C1上不同于A1,A2的任意一点,设直线PA1,PA2的斜率分别为k1,k2.
(1)求椭圆C1的标准方程;
(2)当k1=
,在焦点在x轴上的椭圆C1上求一点Q,使该点到直线PA2的距离最大.
(3)试判断乘积“k1•k2”的值是否与点P的位置有关,并证明你的结论.
| ||
| 2 |
| x2 |
| 3 |
(1)求椭圆C1的标准方程;
(2)当k1=
| 1 |
| 2 |
(3)试判断乘积“k1•k2”的值是否与点P的位置有关,并证明你的结论.
考点:直线与圆锥曲线的综合问题
专题:
分析:(1)求出双曲线
-y2=1的左右焦点为(±2,0),得到椭圆的A1,A2的坐标,设出设椭圆C1的标准方程为
+
=1(a>b>0),求出a,利用e,然后求解b,求出椭圆C1的标准方程.
(2)求出直线PA2的方程为y=-
(x-2)即x+2y-2=0,推出平行线方程与椭圆联立方程组利用判别式为0,求出m值,即可求解点Q坐标满足题意.
(3)设P(x0,y0)则
+y02=1,利用k1k2,化简整理即可求出k1k2的值与点P的位置无关.
| x2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
(2)求出直线PA2的方程为y=-
| 1 |
| 2 |
(3)设P(x0,y0)则
| x02 |
| 4 |
解答:
(13分)
解:(1)双曲线
-y2=1的左右焦点为(±2,0),即A1,A2的坐标分别为(_2,0),(2,0).
∴设椭圆C1的标准方程为
+
=1(a>b>0),则a=2,
且e=
=
,所以c=
,从而b2=a2-c2=1,
∴椭圆C1的标准方程为
+y2=1.或
+
=1.
(2)当k1=
时,k2=-
,故直线PA2的方程为y=-
(x-2)即x+2y-2=0,
与直线PA2平行的直线方程为:x+2y+m=0,(m>0),代入椭圆方程,
可得(2y+m)2+4y2-4=0,即8y2+4my+m2-4=0,
∴△=16m2-32(m2-4)=0,
解得m=2
,
此时y=-
,∴x=-
,
∴点Q(-
,-
).
(3)设P(x0,y0)则
+y02=1,即y02=1-
=
.
k1k2=
•
=
=-
.∴k1k2的值与点P的位置无关,恒为-
.
解:(1)双曲线
| x2 |
| 3 |
∴设椭圆C1的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
且e=
| c |
| a |
| ||
| 2 |
| 3 |
∴椭圆C1的标准方程为
| x2 |
| 4 |
| x2 |
| 4 |
| y2 |
| 16 |
(2)当k1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
与直线PA2平行的直线方程为:x+2y+m=0,(m>0),代入椭圆方程,
可得(2y+m)2+4y2-4=0,即8y2+4my+m2-4=0,
∴△=16m2-32(m2-4)=0,
解得m=2
| 2 |
此时y=-
| ||
| 2 |
| 2 |
∴点Q(-
| 2 |
| ||
| 2 |
(3)设P(x0,y0)则
| x02 |
| 4 |
| x02 |
| 4 |
| 4-x02 |
| 4 |
k1k2=
| y0-0 |
| x0-(-2) |
| y0-0 |
| x0-2 |
| y02 |
| x02-4 |
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题考查椭圆的标准方程的求法,直线与椭圆的位置关系的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
下面说法正确的是( )
| A、不存在既不是奇函数,有又不是偶函数的幂函数 |
| B、图象不经过点(-1,1)的幂函数一定不是偶函数 |
| C、如果两个幂函数的图象有三个公共点,那么这两个幂函数相同 |
| D、如果一个幂函数的图象不与y轴相交,则y=xα中α<0 |
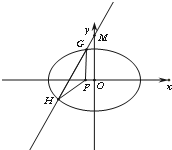 已知椭圆C:
已知椭圆C: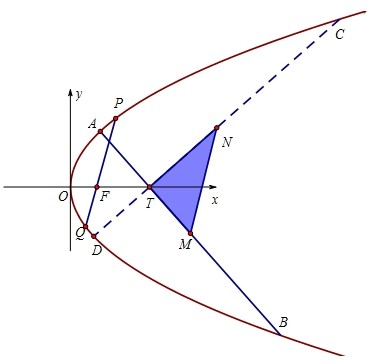
 椭圆G:
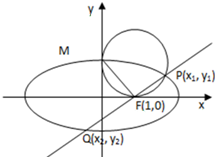
椭圆G: 如图,已知焦点在x轴上的椭圆
如图,已知焦点在x轴上的椭圆