��Ŀ����
2����������{an}��������������T����������������n����an+T=an�������������{an}����TΪ���ڵ��������У���b1=m��0��m��1����������������n����${b_{n+1}}=\left\{{\begin{array}{l}{{b_n}-1\;\;��{b_n}��1����\;\;\;}\\{\frac{1}{b_n}\;\;\;��0��{b_n}��1��}\end{array}}\right.$������{bn}����5Ϊ���ڵ��������У���m��ֵ������$\sqrt{2}$-1����ֻҪ����д����������һ��mֵ���ɣ����� ȡm=$\sqrt{2}$-1=b1��������֤����bn+5=bn��
��� �⣺ȡm=$\sqrt{2}$-1=b1����b2=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1��b3=$\sqrt{2}$��b4=$\sqrt{2}$-1��b5=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1��b6=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1������bn+5=bn��
�ʴ�Ϊ��$\sqrt{2}$-1��
���� ���⿼�������е��ƹ�ϵ�����е������ԣ�������������������������������е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
19��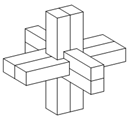 ��ͼΪ�й���ͳ�������³��������Դ�ڹŴ����彨�����״����î�ṹ��������ά��ƴ�������ڲ��İ����֣����î�ṹ�����ϣ���ۿ�����˿�Ϸ��ʮ�������壬�����¡����ҡ�ǰ����ȫ�Գƣ�������ȫ��ͬ�����������ֳ����飬��90���î����������һ³���������������ĵ��������α߳�Ϊ1��������������������ڣ������ڵĺ�Ⱥ��Բ��ƣ����������������������СֵΪ30�У�������������ĸ�Ϊ��������
��ͼΪ�й���ͳ�������³��������Դ�ڹŴ����彨�����״����î�ṹ��������ά��ƴ�������ڲ��İ����֣����î�ṹ�����ϣ���ۿ�����˿�Ϸ��ʮ�������壬�����¡����ҡ�ǰ����ȫ�Գƣ�������ȫ��ͬ�����������ֳ����飬��90���î����������һ³���������������ĵ��������α߳�Ϊ1��������������������ڣ������ڵĺ�Ⱥ��Բ��ƣ����������������������СֵΪ30�У�������������ĸ�Ϊ��������
 ��ͼΪ�й���ͳ�������³��������Դ�ڹŴ����彨�����״����î�ṹ��������ά��ƴ�������ڲ��İ����֣����î�ṹ�����ϣ���ۿ�����˿�Ϸ��ʮ�������壬�����¡����ҡ�ǰ����ȫ�Գƣ�������ȫ��ͬ�����������ֳ����飬��90���î����������һ³���������������ĵ��������α߳�Ϊ1��������������������ڣ������ڵĺ�Ⱥ��Բ��ƣ����������������������СֵΪ30�У�������������ĸ�Ϊ��������
��ͼΪ�й���ͳ�������³��������Դ�ڹŴ����彨�����״����î�ṹ��������ά��ƴ�������ڲ��İ����֣����î�ṹ�����ϣ���ۿ�����˿�Ϸ��ʮ�������壬�����¡����ҡ�ǰ����ȫ�Գƣ�������ȫ��ͬ�����������ֳ����飬��90���î����������һ³���������������ĵ��������α߳�Ϊ1��������������������ڣ������ڵĺ�Ⱥ��Բ��ƣ����������������������СֵΪ30�У�������������ĸ�Ϊ��������| A�� | $2\sqrt{6}$ | B�� | $2\sqrt{7}$ | C�� | $4\sqrt{2}$ | D�� | 5 |