题目内容
7.已知函数f(x)=$\left\{\begin{array}{l}{x,x≥a}\\{{x}^{3}-3x,x<a}\end{array}\right.$若函数g(x)=2f(x)-ax恰有2个不同的零点,则实数a的取值范围是(-$\frac{3}{2}$,2).分析 求出g(x)的解析式,计算g(x)的零点,讨论g(x)在区间[a,+∞)上的零点个数,得出g(x)在(-∞,a)上的零点个数,列出不等式解出a的范围.
解答 解:g(x)=$\left\{\begin{array}{l}{(2-a)x,x≥a}\\{2{x}^{3}-(6+a)x,x<a}\end{array}\right.$,
显然,当a=2时,g(x)有无穷多个零点,不符合题意;
当x≥a时,令g(x)x=0得x=0,
当x<a时,令g(x)=0得x=0或x2=$\frac{6+a}{2}$,
(1)若a>0且a≠2,则g(x)在[a,+∞)上无零点,在(-∞,a)上存在零点x=0和x=-$\sqrt{\frac{6+a}{2}}$,
∴$\sqrt{\frac{6+a}{2}}$≥a,解得0<a<2,
(2)若a=0,则g(x)在[0,+∞)上存在零点x=0,在(-∞,0)上存在零点x=-$\sqrt{\frac{6}{2}}$,
符合题意;
(3)若a<0,则g(x)在[a,+∞)上存在零点x=0,
∴g(x)在(-∞,a)上只有1个零点,∵0∉(-∞,a),∴g(x)在(-∞,a)上的零点为x=-$\sqrt{\frac{6+a}{2}}$,
∴-$\sqrt{\frac{6+a}{2}}$<a,解得-$\frac{3}{2}$<a<0.
综上,a的取值范围是(-$\frac{3}{2}$,2).
故答案为(-$\frac{3}{2}$,2).
点评 本题考查了函数零点的个数判断,分类讨论思想,属于中档题.

练习册系列答案
相关题目
15.在△ABC中,角A,B,C的对边分别为a,b,c,已知∠B=30°,△ABC的面积为$\frac{3}{2}$,且sinA+sinC=2sinB,则b的值为( )
| A. | 4+2$\sqrt{3}$ | B. | 4-2$\sqrt{3}$ | C. | $\sqrt{3}$-1 | D. | $\sqrt{3}$+1 |
19.设全集U是实数集R,已知集合A={x|x2>2x},B={x|log2(x-1)≤0},则(∁UA)∩B=( )
| A. | {x|1<x<2} | B. | {x|1≤x<2} | C. | {x|1<x≤2} | D. | {x|1≤x≤2} |
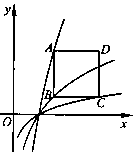 如图,已知正方形ABCD的边长为2,BC平行于x轴,顶点A,B和C分别在函数y1=3logax,y2=2logax和y3=logax(a>1)的图象上,则实数a的值为$\sqrt{2}$.
如图,已知正方形ABCD的边长为2,BC平行于x轴,顶点A,B和C分别在函数y1=3logax,y2=2logax和y3=logax(a>1)的图象上,则实数a的值为$\sqrt{2}$.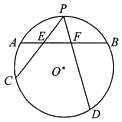 如图,已知AB为圆O的一条弦,点P为弧$\widehat{AB}$的中点,过点P任作两条弦PC,PD分别交AB于点E,F
如图,已知AB为圆O的一条弦,点P为弧$\widehat{AB}$的中点,过点P任作两条弦PC,PD分别交AB于点E,F