题目内容

12．函数$f（x）=\frac{{1+{e^x}}}{{1-{e^x}}}$（其中e是自然对数的底数）的大致图象为（　　）
A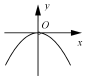．B．C．D．

分析 求出定义域，再判断f（x）的符号即可得出答案．

解答 解：由1-ex≠0可得x≠0，排除A，C；
当x＜0时，0＜ex＜1，∴f（x）=$\frac{1+{e}^{x}}{1-{e}^{x}}$＞0，排除B，
故选D．

点评 本题考查了函数的图象判断，属于中档题．

练习册系列答案
相关题目
2．对于数列{an}，若存在正整数T，对于任意正整数n都有an+T=an成立，则称数列{an}是以T为周期的周期数列．设b1=m（0＜m＜1），对任意正整数n都有${b_{n+1}}=\left\{{\begin{array}{l}{{b_n}-1\;\;（{b_n}＞1），\;\;\;}\\{\frac{1}{b_n}\;\;\;（0＜{b_n}≤1）}\end{array}}\right.$若数列{bn}是以5为周期的周期数列，则m的值可以是$\sqrt{2}$-1．（只要求填写满足条件的一个m值即可）
3．设复数z=a+bi（a，b∈R，b＞0），且$\overline z={z^2}$，则z的虚部为（　　）
A．$\frac{1}{2}$B．$\frac{{\sqrt{2}}}{2}$C．$\frac{{\sqrt{3}}}{2}$D．$\frac{3}{2}$
20．已知角A，B，C为等腰△ABC的内角，设向量$\overrightarrow{m}$=（2sinA-sinC，sinB），$\overrightarrow{n}$=（cosC，cosB），且$\overrightarrow{m}$∥$\overrightarrow{n}$，BC=$\sqrt{7}$
（Ⅰ）求角B；
（Ⅱ）在△ABC的外接圆的劣弧$\widehat{AC}$上取一点D，使得AD=1，求sin∠DAC及四边形ABCD的面积．
7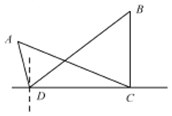．如图所示，为了测量A，B处岛屿的距离，小明在D处观测，A，B分别在D处的北偏西15°、北偏东45°方向，再往正东方向行驶40海里至C处，观测B在C处的正北方向，A在C处的北偏西60°方向，则A，B两处岛屿间的距离为（　　）
A．$20\sqrt{6}$海里B．$40\sqrt{6}$海里C．$20（1+\sqrt{3}）$海里D．40海里
17．已知数列{an}的前n项和为Sn，a1=$\frac{3}{4}$，Sn=Sn-1+an-1+$\frac{1}{2}$（n∈N*且n≥2），数列{bn}满足：b1=-$\frac{37}{4}$，且3bn-bn-1=n+1（n∈N*且n≥2）．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求证：数列{bn-an}为等比数列；
（Ⅲ）求数列{bn}的前n项和的最小值．
4．在平面直角坐标系中，角α的顶点与原点O重合，始边与x轴的非负半轴重合，点P（-2t，t）（t≠0）是角α终边上的一点，则$tan（α+\frac{π}{4}）$的值为（　　）
A．$3-2\sqrt{2}$B．3C．$-\frac{1}{3}$D．$\frac{1}{3}$
1．若函数f（x）=1nx-$\frac{1}{e^2}$x+a有零点，则实数a的取值范围是（　　）
A．（-∞，-1]B．（-∞，1]C．[-1，+∞）D．[1，+∞）
2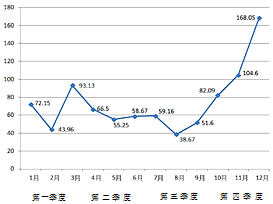．北京市2016年12个月的PM2.5平均浓度指数如图所示．由图判断，四个季度中PM2.5的平均浓度指数方差最小的是（　　）
A．第一季度B．第二季度C．第三季度D．第四季度

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网