题目内容
定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期为π,且当x∈[-
,0)时,f(x)=sin x,则f(-
)的值为( )
| π |
| 2 |
| 2π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点:函数的周期性,函数的值
专题:函数的性质及应用
分析:由已知中函数f(x)既是偶函数又是周期函数,且函数f(x)既是偶函数又是周期函数,故f(-
)=f(
)=f(-
),进而结合当x∈[-
,0)时,f(x)=sin x,得到答案.
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
解答:
解:∵x∈[-
,0)时,f(x)=sin x,
∴f(-
)=sin(-
)=-
,
∵函数f(x)既是偶函数又是周期函数,且f(x)的最小正周期为π,
∴f(-
)=f(
)=f(-
)=-
,
故选:C
| π |
| 2 |
∴f(-
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
∵函数f(x)既是偶函数又是周期函数,且f(x)的最小正周期为π,
∴f(-
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
故选:C
点评:本题考查的知识点是函数的值,函数的周期性,函数的奇偶性,其中由已知得到f(-
)=f(
)=f(-
),是解答的关键.
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |

练习册系列答案
相关题目
执行如图所示的程序框图,其输出的结果是( )


| A、1 | ||
B、-
| ||
C、-
| ||
D、-
|
函数f(x)=(
) x2+2(a-1)x+2在区间(-∞,4]上单调递增,那么实数a的取值范围是( )
| 1 |
| 2 |
| A、a≤-3 | B、a≥-3 |
| C、a≤5 | D、a≥5 |
已知O,A,B,C四点共面,直线OA是线段BC的垂直平分线,
=a,
=b,则
=( )
| OA |
| OB |
| OC |
A、(
| ||||||||||||
B、2(
| ||||||||||||
C、(
| ||||||||||||
D、2(
|
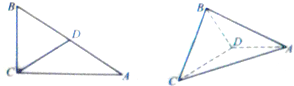 在Rt△ABC中,BC=2,AB=4,∠ACB=90°,D为边AB的中点,沿CD把△BCD折起,使平面BCD⊥平面ACD.
在Rt△ABC中,BC=2,AB=4,∠ACB=90°,D为边AB的中点,沿CD把△BCD折起,使平面BCD⊥平面ACD. 已知某几何体的三视图如图所示,其中侧视图是边长为2的正三角形,正视图是矩形,且AA1=4,则此几何体的体积为
已知某几何体的三视图如图所示,其中侧视图是边长为2的正三角形,正视图是矩形,且AA1=4,则此几何体的体积为