题目内容
解下列关于x的方程：
（1）sin4x=sin
；
（2）sinxcosx+sin2x-2cos2x=0；
（3）3sin2x+8sinxcosx-3cos2x=5．
（1）sin4x=sin
| π |
| 12 |
（2）sinxcosx+sin2x-2cos2x=0；
（3）3sin2x+8sinxcosx-3cos2x=5．
考点：三角函数的化简求值
专题：三角函数的求值
分析：（1）直接利用三角方程求解sin4x=sin
；
（2）化简sinxcosx+sin2x-2cos2x=0；为正切函数的方程，然后利用反三角函数求出方程的解即可．
（3）利用同角三角函数的基本关系式化简3sin2x+8sinxcosx-3cos2x=5．为正切形式的方程，然后求解即可．
| π |
| 12 |
（2）化简sinxcosx+sin2x-2cos2x=0；为正切函数的方程，然后利用反三角函数求出方程的解即可．
（3）利用同角三角函数的基本关系式化简3sin2x+8sinxcosx-3cos2x=5．为正切形式的方程，然后求解即可．
解答：
解：（1）sin4x=sin
；可得4x=2kπ+
，或4x=2kπ+
，k∈Z，
即x=
+
或x=
+
，k∈Z．
（2）由sinxcosx+sin2x-2cos2x=0得：tan2x+tanx-2=0，
解得：tanx=1或tanx=-2，
故x=kπ+
，或x=kπ-arctan2，k∈Z．
（3）3sin2x+8sinxcosx-3cos2x=5．
即：2sin2x-8sinxcosx+8cos2x=0，
即：2tan2x-8tanx+8=0，
解得：tanx=2，于是x=kπ+arctan2，k∈Z．
| π |
| 12 |
| π |
| 12 |
| 11π |
| 12 |
即x=
| kπ |
| 2 |
| π |
| 48 |
| kπ |
| 2 |
| 11π |
| 48 |
（2）由sinxcosx+sin2x-2cos2x=0得：tan2x+tanx-2=0，
解得：tanx=1或tanx=-2，
故x=kπ+
| π |
| 4 |
（3）3sin2x+8sinxcosx-3cos2x=5．
即：2sin2x-8sinxcosx+8cos2x=0，
即：2tan2x-8tanx+8=0，
解得：tanx=2，于是x=kπ+arctan2，k∈Z．
点评：本题主要考查三角函数的化简求值．解决此类问题的关键在于对公式的熟练掌握及灵活运用．
练习册系列答案
阅读快车系列答案
相关题目
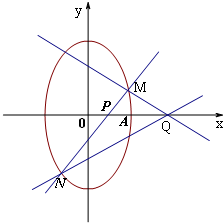已知椭圆C：