题目内容
某人沿一条折线段组成的小路前进,从A到B,方位角(从正北方向顺时针转到AB方向所成的角)是50°,距离是3km;从B到C,方位角是110°,距离是3km;从C到D,方位角是140°,距离是(9+3
)km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
| 3 |
考点:解三角形的实际应用
专题:应用题,解三角形
分析:作出示意图,连接AC,在△ABC中,由余弦定理求出AC,在△ACD中,由余弦定理求出AD,从而可求∠CAD,即可得出结论.
解答:
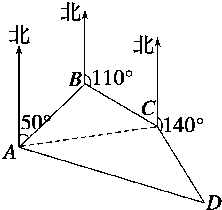 解:示意图,如图所示,(4分)
解:示意图,如图所示,(4分)
连接AC,在△ABC中,∠ABC=50°+(180°-110°)=120°,
又AB=BC=3,∴∠BAC=∠BCA=30°
由余弦定理可得AC=
=3
(7分)
在△ACD中,∠ACD=360°-140°-(70°+30°)=120°,
CD=3
+9.
由余弦定理得AD=
=
(km).(10分)
由正弦定理得sin∠CAD=
=
(12分)
∴∠CAD=45°,于是AD的方位角为50°+30°+45°=125°,(13分)
∴从A到D的方位角是125°,距离为
km.(14分)
 解:示意图,如图所示,(4分)
解:示意图,如图所示,(4分)连接AC,在△ABC中,∠ABC=50°+(180°-110°)=120°,
又AB=BC=3,∴∠BAC=∠BCA=30°
由余弦定理可得AC=
| AB2+BC2-2AB•BC•cos120° |
| 3 |
在△ACD中,∠ACD=360°-140°-(70°+30°)=120°,
CD=3
| 3 |
由余弦定理得AD=
| AC2+CD2-2AC•CD•cos120° |
=
9(
| ||||
| 2 |
由正弦定理得sin∠CAD=
| CD•sin∠ACD |
| AD |
| ||
| 2 |
∴∠CAD=45°,于是AD的方位角为50°+30°+45°=125°,(13分)
∴从A到D的方位角是125°,距离为
9(
| ||||
| 2 |
点评:本题考查解三角形的实际应用,考查余弦定理、正弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
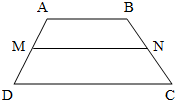 用向量法证明:梯形的中位线平行于两底边且等于两底边和的一半.
用向量法证明:梯形的中位线平行于两底边且等于两底边和的一半.