题目内容
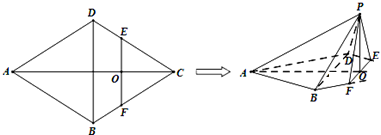
如图所示,在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别是边CD,CB的中点,EF∩AC=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到五棱锥P-ABFED,且PB=
.
(1)求证:BD⊥平面POA;
(2)求二面角B-AP-O的正切值.
| 10 |
(1)求证:BD⊥平面POA;
(2)求二面角B-AP-O的正切值.

考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得BD∥EF,BD⊥AC,从而EF⊥AC,EF⊥AO,EF⊥PO,由此能证明BD⊥平面POA.
(2)设AO∩BD=H,连结BO,则△ABD是等边三角形,从而BD=4,BH=2,HA=2
,HO=PO=
,BO=
,进而PO⊥BO,PO⊥平面BFED,过H作HG⊥AP,垂足为G,连结BG,∠BGH为二面角B-AP-O的平面角,由此能求出二面角B-AP-O的正切值.
(2)设AO∩BD=H,连结BO,则△ABD是等边三角形,从而BD=4,BH=2,HA=2
| 3 |
| 3 |
| 7 |
解答:
(1)证明:∵点E,F分别是边CD、CB的中点,
∴BD∥EF,
∴菱形ABCD的对角线互相垂直,
∴BD⊥AC,∴EF⊥AC,
∴EF⊥AO,EF⊥PO,
∵AO?平面POA,PO?平面POA,AO∩PO=O,
∴EF⊥平面POA,∴BD⊥平面POA.
(2)解:设AO∩BD=H,连结BO,
∵∠DAB=60°,∴△ABD是等边三角形,
∴BD=4,BH=2,HA=2
,HO=PO=
,
在Rt△BHO中,BO=
=
,
在PBO中,BO2+PO2=10=PB2,
∴PO⊥BO,
∵PO⊥EF,EF∩BO=O,EF?平面BFED,
∴PO⊥平面BFED,
过H作HG⊥AP,垂足为G,连结BG,
由(1)知BH⊥平面POA,且AP?平面POA,
∴BH⊥AP,
∵HG∩BH=H,HG?平面BHG,BH?平面BHG,
∴AP⊥平面BHG,BG?平面BHG,
∵BG?平面BHG,∴AP⊥BG,
∴∠BGH为二面角B-AP-O的平面角,
在Rt△POA中,AP=
=
,
在Rt△POA和Rt△HGA\中,∠POA=∠HGA=90°,∠APO=∠HAG,
∴△POA∽△HGA,∴
=
,
∴HG=
=
=
.
在Rt△BHG中,tan∠BGH=
=
=
.
∴二面角B-AP-O的正切值为
.
∴BD∥EF,
∴菱形ABCD的对角线互相垂直,
∴BD⊥AC,∴EF⊥AC,
∴EF⊥AO,EF⊥PO,
∵AO?平面POA,PO?平面POA,AO∩PO=O,
∴EF⊥平面POA,∴BD⊥平面POA.

(2)解:设AO∩BD=H,连结BO,
∵∠DAB=60°,∴△ABD是等边三角形,
∴BD=4,BH=2,HA=2
| 3 |
| 3 |
在Rt△BHO中,BO=
| BH2+HO2 |
| 7 |
在PBO中,BO2+PO2=10=PB2,
∴PO⊥BO,
∵PO⊥EF,EF∩BO=O,EF?平面BFED,
∴PO⊥平面BFED,
过H作HG⊥AP,垂足为G,连结BG,
由(1)知BH⊥平面POA,且AP?平面POA,
∴BH⊥AP,
∵HG∩BH=H,HG?平面BHG,BH?平面BHG,
∴AP⊥平面BHG,BG?平面BHG,
∵BG?平面BHG,∴AP⊥BG,
∴∠BGH为二面角B-AP-O的平面角,
在Rt△POA中,AP=
| AO2+PO2 |
| 30 |
在Rt△POA和Rt△HGA\中,∠POA=∠HGA=90°,∠APO=∠HAG,
∴△POA∽△HGA,∴
| PO |
| HG |
| PA |
| HA |
∴HG=
| PO•HA |
| PA |
| ||||
|
| ||
| 5 |
在Rt△BHG中,tan∠BGH=
| BH |
| HG |
| 2 | ||||
|
| ||
| 3 |
∴二面角B-AP-O的正切值为
| ||
| 3 |
点评:本题考查空间线面关系、二面角、空间向量及坐标运算等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在空间直角坐标系中有直三棱柱ABCA1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为
如图所示,在空间直角坐标系中有直三棱柱ABCA1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为 如图,抛物线y=ax2-
如图,抛物线y=ax2- 已知空间四边形ABCD中,AB⊥CD,AB=4,CD=4
已知空间四边形ABCD中,AB⊥CD,AB=4,CD=4 如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.
如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S. 经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其他鱼偏高.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm,现从一批数量很大的罗非鱼中随机地抽出15条作为样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后第一位数字为叶)如图所示
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其他鱼偏高.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm,现从一批数量很大的罗非鱼中随机地抽出15条作为样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后第一位数字为叶)如图所示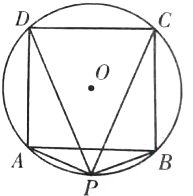 如图,设四边形ACBD是⊙O的内接正方形,P是⊙O上的任一点,求证:|
如图,设四边形ACBD是⊙O的内接正方形,P是⊙O上的任一点,求证:|