题目内容
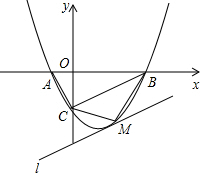
 如图,抛物线y=ax2-
如图,抛物线y=ax2-| 3 |
| 2 |
(1)求抛物线的解析式
(2)试判断△ABC的形状,并说明
(3)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标.
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.
(2)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
(3)△MBC的面积可由S△MBC=
BC×h表示,若要它的面积最大,需要使h取最大值,即点M到直线BC的距离最大,若设一条平行于BC的直线,那么当该直线与抛物线有且只有一个交点时,该交点就是点M.
(2)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
(3)△MBC的面积可由S△MBC=
| 1 |
| 2 |
解答:
解:(1)B(4,0)代入,可得16a-6-2=0,∴a=
,
∴抛物线的解析式y=
x2-
x-2;
(2)由(1)的函数解析式可求得:A(-1,0)、C(0,-2);
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,又:OC⊥AB,
∴△OAC∽△OCB,得:∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形;
(3)已求得:B(4,0)、C(0,-2),可得直线BC的解析式为:y=
x-2;
设直线l∥BC,则该直线的解析式可表示为:y=
x+b,当直线l与抛物线只有一个交点时,可列方程:
x+b=
x2-
x-2,即:
x2-2x-2-b=0,且△=0;
∴4-4×
(-2-b)=0,即b=-4;
∴直线l:y=
x-4.
所以点M即直线l和抛物线的唯一交点,有:
,解得:x=2,y=-3
即M(2,-3).
过M点作MN⊥x轴于N,
S△BMC=S梯形OCMN+S△MNB-S△OCB=
×2×(2+3)+
×2×3-
×2×4=4.
| 1 |
| 2 |
∴抛物线的解析式y=
| 1 |
| 2 |
| 3 |
| 2 |
(2)由(1)的函数解析式可求得:A(-1,0)、C(0,-2);
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,又:OC⊥AB,
∴△OAC∽△OCB,得:∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形;
(3)已求得:B(4,0)、C(0,-2),可得直线BC的解析式为:y=
| 1 |
| 2 |
设直线l∥BC,则该直线的解析式可表示为:y=
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴4-4×
| 1 |
| 2 |
∴直线l:y=
| 1 |
| 2 |
所以点M即直线l和抛物线的唯一交点,有:
|
即M(2,-3).
过M点作MN⊥x轴于N,
S△BMC=S梯形OCMN+S△MNB-S△OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查抛物线方程,该题的难度不算太大,但用到的琐碎知识点较多,综合性很强.熟练掌握直角三角形的相关性质以及三角形的面积公式是理出思路的关键.

练习册系列答案
相关题目
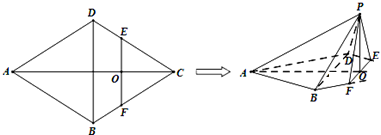
把边长为2的正三角形ABC沿BC边上的高AD折成直二面角,设折叠后BC中点为M,则AC与DM所成角的余弦值为
( )
( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
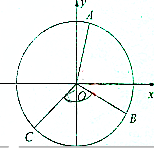 如图,在平面直角坐标系xOy中,单位圆上的A、B两点分别在第一、四象限,已知A、B两点的纵坐标分别为
如图,在平面直角坐标系xOy中,单位圆上的A、B两点分别在第一、四象限,已知A、B两点的纵坐标分别为