题目内容
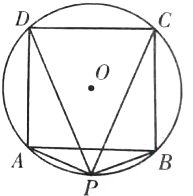如图，设四边形ACBD是⊙O的内接正方形，P是⊙O上的任一点，求证：|| PA |
| PB |
| PC |
| PD |
考点：向量在几何中的应用
专题：平面向量及应用
分析：把正方形的2条对角线对应的向量分别用向量
，
，
来表示，直角三角形中利用向量法求出2条对角线长度的平方和，即可得结论．
| PA |
| PB， |
| PC |
| PD |
解答：
解：因为
=
-
，
=
-
，
因为四边形ACBD是⊙O的内接正方形，P是⊙O上的任一点，所以
⊥
，
⊥
，
⊥
，
所以
2=
2+
2，
2=
2+
2，
所以：|
|2+|
|2+|
|2+|
|2=
2+
2=8r2，r是圆的半径；P是圆上任意一点．
| BD |
| PD |
| PB |
| AC |
| PC |
| PA |
因为四边形ACBD是⊙O的内接正方形，P是⊙O上的任一点，所以
| AC |
| BD |
| PB |
| PD |
| PC |
| PA |
所以
| BD |
| PD |
| PB |
| AC |
| PC |
| PA |
所以：|
| PA |
| PB |
| PC |
| PD |
| BD |
| AC |
点评：本题考查向量在几何中的应用，利用线段长度的平方等于对应向量的平方．
练习册系列答案
名校课堂系列答案
相关题目
