题目内容
求下列函数的导数:
(1)y=23x-1
(2)y=log2(2-4x)
(1)y=23x-1
(2)y=log2(2-4x)
考点:导数的运算
专题:导数的概念及应用
分析:根据导数的求导法则进行求导即可.
解答:
解:(1)y=23x-1=
•8x,
则函数的导数f′(x)=
•8xln8,
(2)∵y=log2(2-4x),
∴y′=
•(-4)=-
.
| 1 |
| 2 |
则函数的导数f′(x)=
| 1 |
| 2 |
(2)∵y=log2(2-4x),
∴y′=
| 1 |
| (2-4x)ln2 |
| 4 |
| (2-4x)ln2 |
点评:本题主要考查函数的导数的计算,要求熟练掌握掌握常见函数的导数公式,比较基础.

练习册系列答案
相关题目
已知各项均为正数的等比数列{an}满足a1a2a3a4=6,a7a8a9a10=6
,则a13a14a15a16=( )
| 3 |
| A、18 | ||
B、10
| ||
| C、10 | ||
D、
|
下列函数中,在(-1,1)内有零点且单调递增的是( )
| A、y=log2x |
| B、y=2x-1 |
| C、y=x2-2 |
| D、y=-x3 |
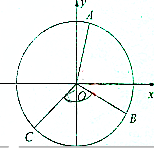 如图,在平面直角坐标系xOy中,单位圆上的A、B两点分别在第一、四象限,已知A、B两点的纵坐标分别为
如图,在平面直角坐标系xOy中,单位圆上的A、B两点分别在第一、四象限,已知A、B两点的纵坐标分别为