题目内容
已知函数f(x)=
,若存在实数x1,x2,x3,x4,满足x1<x2<x3<x4,且f(x1)=f(x2)=f(x3)=f(x4),则
的取值范围是( )
|
| (x3-2)•(x4-2) |
| x1•x2 |
| A、(0,12) |
| B、(4,16) |
| C、(9,21) |
| D、(15,25) |
考点:分段函数的应用
专题:计算题,数形结合,函数的性质及应用
分析:画出函数f(x)的图象,确定x1x2=1,x3+x4=12,2<x3<4,8<x4<10,由此可得
的取值范围.
| (x3-2)•(x4-2) |
| x1•x2 |
解答:
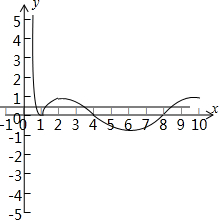 解:函数的图象如图所示,
解:函数的图象如图所示,
∵f(x1)=f(x2),
∴-log2x1=log2x2,
∴log2x1x2=0,
∴x1x2=1,
∵f(x3)=f(x4),
∴x3+x4=12,2<x3<x4<10
∴
=x3x4-2(x3+x4)+4=x3x4-20,
∵2<x3<4,8<x4<10
∴
的取值范围是(0,12).
故选:A.
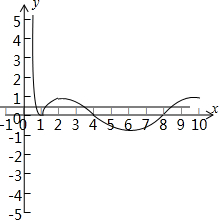 解:函数的图象如图所示,
解:函数的图象如图所示,∵f(x1)=f(x2),
∴-log2x1=log2x2,
∴log2x1x2=0,
∴x1x2=1,
∵f(x3)=f(x4),
∴x3+x4=12,2<x3<x4<10
∴
| (x3-2)•(x4-2) |
| x1•x2 |
∵2<x3<4,8<x4<10
∴
| (x3-2)•(x4-2) |
| x1•x2 |
故选:A.
点评:本小题主要考查分段函数的解析式求法及其图象的作法、函数的值域的应用、函数与方程的综合运用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.

练习册系列答案
相关题目
一物体在力F(x)=3x+4的作用下,沿着与力F相同的方向,从x=0处运动到x=4处,则力F所作的功是( )
| A、14 | B、40 | C、3 | D、12 |
已知集合A∪B={1,2,3},A={1}则B的子集最多可能有( )
| A、5个 | B、6个 | C、7个 | D、8个 |
f(x)=x3+
+1,若f(a)=2,则f(-a)的值为( )
| 3 | x |
| A、3 | B、0 | C、-1 | D、-2 |
在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0),若ξ在(0,2)内取值的概率为0.4,则ξ在(0,+∞)内取值的概率为( )
| A、0.2 | B、0.4 |
| C、0.8 | D、0.9 |
 如图所示,图中有5组数据,去掉
如图所示,图中有5组数据,去掉