题目内容
已知x+y=1,y>0,x≠0,则
+
最小值为 .
| 1 |
| 2|x| |
| |x| |
| y+1 |
考点:函数的最值及其几何意义
专题:不等式的解法及应用
分析:根据条件利用消元法,转化为关于x的式子,利用基本不等式的性质即可求出式子的最值.
解答:
解:由x+y=1,y>0得y=1-x>0,
解得x<1且x≠0.
①当0<x<1时,
+
=
+
=
+
=
+
=
+
+
≥
+2
=
+2
=
+1=
,
当且仅当
=
,即x=
时取等号,此时的最小值
.
②当x<0时,
+
=
-
=
+
=
+
-
,
∵x<0,∴-x>0,2-x>0,
∴
+
=
+
-
≥2
-
=1-
=
,当且仅当-
=-
,
即(2-x)2=4x2,即3x2+4x-4=0,解得x=-2或x=
(舍)时,取得号,此时最小值为
,
综上
+
最小值为
,
故答案为:
解得x<1且x≠0.
①当0<x<1时,
| 1 |
| 2|x| |
| |x| |
| y+1 |
| 1 |
| 2x |
| x |
| y+1 |
| 1 |
| 2x |
| x |
| 2-x |
| x+2-x |
| 4x |
| x |
| 2-x |
| 1 |
| 4 |
| 2-x |
| 4x |
| x |
| 2-x |
| 1 |
| 4 |
|
| 1 |
| 4 |
|
| 1 |
| 4 |
| 5 |
| 4 |
当且仅当
| 2-x |
| 4x |
| x |
| 2-x |
| 2 |
| 3 |
| 5 |
| 4 |
②当x<0时,
| 1 |
| 2|x| |
| |x| |
| y+1 |
| 1 |
| -2x |
| x |
| 2-x |
| 2-x+x |
| -4x |
| -x |
| 2-x |
| 2-x |
| -4x |
| -x |
| 2-x |
| 1 |
| 4 |
∵x<0,∴-x>0,2-x>0,
∴
| 1 |
| 2|x| |
| |x| |
| y+1 |
| 2-x |
| -4x |
| -x |
| 2-x |
| 1 |
| 4 |
|
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 2-x |
| 4x |
| x |
| 2-x |
即(2-x)2=4x2,即3x2+4x-4=0,解得x=-2或x=
| 2 |
| 3 |
| 3 |
| 4 |
综上
| 1 |
| 2|x| |
| |x| |
| y+1 |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题主要考查式子最值的求解,根据条件结合基本不等式的应用是解决本题的关键.综合性较强,有一点的难度.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
过定点P(2,1),且倾斜角是直线l:x-y-1=0的倾斜角两倍的直线方程为( )
| A、x-2y-1=0 |
| B、2x-y-1=0 |
| C、y-1=2(x-2) |
| D、x=2 |
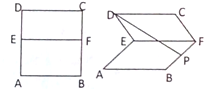 已知E,F是正方形ABCD的边AD,BC中点,P是BF的中点,如图将该正方形以EF为棱折成60°的二面角D-EF-A,则直线DP和平面ABFE所成角的正切值是
已知E,F是正方形ABCD的边AD,BC中点,P是BF的中点,如图将该正方形以EF为棱折成60°的二面角D-EF-A,则直线DP和平面ABFE所成角的正切值是