题目内容
双曲线C：
-
=1（a＞0，b＞0）的左右焦点分别为F1、F2，离心率为
，过F1且与x轴垂直的直线与双曲线C交于A，B两点，则|AF1|与|AF2|的关系是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、2|AF2|=3|AF1| |
| B、|AF2|=2|AF1| |
| C、|AF2|=3|AF1| |
| D、3|AF2|=4|AF1| |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由离心率公式可得c=
a，b2=c2-a2=2a2，令x=-c，可得|AF1|=2a，再也双曲线的定义可得|AF2|，即可得到结论．
| 3 |
解答：
解：双曲线C：
-
=1的左右焦点分别为F1（-c，0），F2（c，0），
则由题意可得e=
=
，即有c=
a，b2=c2-a2=2a2，
令x=-c，则y2=b2（
-1）=2b2=4a2，即有|AF1|=2a，
由双曲线的定义，可得|AF2|-|AF1|=2a，即有|AF2|=4a，
则有|AF2|=2|AF1|．
故选B．
| x2 |
| a2 |
| y2 |
| b2 |
则由题意可得e=
| c |
| a |
| 3 |
| 3 |
令x=-c，则y2=b2（
| c2 |
| a2 |
由双曲线的定义，可得|AF2|-|AF1|=2a，即有|AF2|=4a，
则有|AF2|=2|AF1|．
故选B．
点评：本题考查双曲线的定义、方程和性质，考查运算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=ln|x-2|-m（m∈R）的所有零点之和为（ ）
| A、-4 | B、2 |
| C、4 | D、与实数m有关 |
已知△ABC，∠A=120°，
•
=-2，
=
，点G是CD 上的一点，
=
+m
，则|
|的最小值为（ ）
| AB |
| AC |
| AD |
| 1 |
| 2 |
| AB |
| AG |
| 1 |
| 3 |
| AB |
| AC |
| AG |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
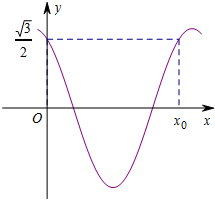函数f（x）=cos（πx+φ）（0＜φ＜