题目内容
已知等差数列{an}的前n项和Sn=48,S2n=60,则S3n= .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由等差数列性质可得Sn,S2n-Sn,S3n-S2n…仍为等差数列,结合题中的条件易得答案.
解答:
解:∵数列{an}为等差数列,
∴Sn,S2n-Sn,S3n-S2n…为等差数列.
即48,12,S3n-60成等差数列,
∴2×12=48+S3n-60,解得S3n=36,
故答案为:36
∴Sn,S2n-Sn,S3n-S2n…为等差数列.
即48,12,S3n-60成等差数列,
∴2×12=48+S3n-60,解得S3n=36,
故答案为:36
点评:本题考查等差数列的前n项和的性质,得出Sn,S2n-Sn,S3n-S2n…仍为等差数列是解决问题的关键,属基础题.

练习册系列答案
相关题目
某大型表演中,需要把200人排成一人数前哨少后多的梯形对阵,梯形对阵排数大于3排,且要求各行的人数必须是连续的自然数,这样才能使后一排的人均站在前一排两人间的空档处,那么,满足上述要求的排法的方案有( )
| A、1种 | B、2种 | C、4种 | D、0种 |
在斜三角形ABC中,“A>B”是“|tanA|>|tanB|”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
集合M={1,2,3}的真子集个数为( )
| A、6 | B、7 | C、8 | D、9 |
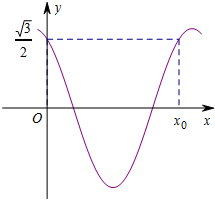 函数f(x)=cos(πx+φ)(0<φ<
函数f(x)=cos(πx+φ)(0<φ<