题目内容
3.设x,y为正实数,且x+y=1,则$\frac{4}{x}$+$\frac{1}{y}$的最小值为( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 由题意整体代入可得$\frac{4}{x}$+$\frac{1}{y}$=($\frac{4}{x}$+$\frac{1}{y}$)(x+y)=5+$\frac{4y}{x}$+$\frac{x}{y}$,由基本不等式可得.
解答 解:∵x,y为正实数,且x+y=1,
∴$\frac{4}{x}$+$\frac{1}{y}$=($\frac{4}{x}$+$\frac{1}{y}$)(x+y)
=5+$\frac{4y}{x}$+$\frac{x}{y}$≥5+2$\sqrt{\frac{4y}{x}•\frac{x}{y}}$=9
当且仅当$\frac{4y}{x}$=$\frac{x}{y}$即x=$\frac{2}{3}$且y=$\frac{1}{3}$时取等号.
故选:A
点评 本题考查基本不等式求最值,整体代入是解决问题的关键,属基础题.

练习册系列答案
相关题目
11.如果$0<{log_{\frac{1}{2}}}x$$<{log_{\frac{1}{2}}}y$,那么( )
| A. | 0<y<x<1 | B. | 0<x<y<1 | C. | y>x>1 | D. | x>y>1 |
18.直线y=x+b与曲线x=-$\sqrt{1-y^2}$有且只有一个交点,则b的取值范围是( )
| A. | |b|=$\sqrt{2}$ | B. | -1≤b<1,或b=$\sqrt{2}$ | C. | -1≤b≤1 | D. | 非A,B,C结论 |
8.定义:底面是正三角形,侧棱与底面垂直的三棱柱叫做正三棱柱,将正三棱柱截去一个角,(如图1所示,M,N分别为AB,BC的中点)得到几何体如图2.则该几何体按图2所示方向的侧视图为( )
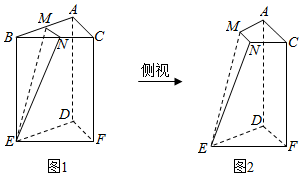

| A. | 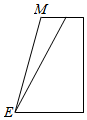 | B. | 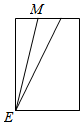 | C. | 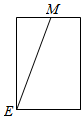 | D. |  |
12.下列各组函数相等的是( )
| A. | $f(x)=\frac{{{x^2}-1}}{x-1}与g(x)=x+1$ | B. | $f(x)=1与g(x)=\frac{{\sqrt{x^2}}}{x}$ | ||
| C. | f(x)=(x-2)0与g(x)=1 | D. | $f(x)=\sqrt{x^4}与g(x)={x^2}$ |
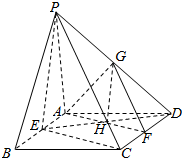 如图,四棱锥P-ABCD的底面是平行四边形,PA=PB=AB=2,E,F分别是AB,CD的中点,平面AGF∥平面PEC,PD∩平面AGF=G,ED与AF相交于点H,则GH=$\frac{\sqrt{3}}{2}$.
如图,四棱锥P-ABCD的底面是平行四边形,PA=PB=AB=2,E,F分别是AB,CD的中点,平面AGF∥平面PEC,PD∩平面AGF=G,ED与AF相交于点H,则GH=$\frac{\sqrt{3}}{2}$.