题目内容
19.函数y=1g(tan2x)的定义域是( )| A. | (kπ,kπ+$\frac{π}{2}$)(k∈Z) | B. | (2kπ,2kπ+$\frac{π}{2}$)(k∈Z) | C. | ($\frac{1}{2}$kπ,$\frac{1}{2}$kπ+$\frac{π}{2}$)(k∈Z) | D. | ($\frac{1}{2}$kπ,$\frac{1}{2}$kπ+$\frac{π}{4}$)(k∈Z) |
分析 根据对数函数的真数大于0,列出不等式tan2x>0,求出解集即可.
解答 解:∵函数y=1g(tan2x),
∴tan2x>0,
∴kπ<2x<$\frac{π}{2}$+kπ,k∈Z,
∴$\frac{kπ}{2}$<x<$\frac{π}{4}$+$\frac{kπ}{2}$,k∈Z;
∴函数y=lg(tan2x)的定义域是($\frac{kπ}{2}$,$\frac{π}{4}$+$\frac{kπ}{2}$),k∈Z.
故选:D.
点评 本题考查了对数函数的定义以及解三角函数不等式的应用问题,是基础题目.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.已知x,y满足约柬条件$\left\{\begin{array}{l}{x-y-1≤0}\\{2x-y-3≥0}\end{array}\right.$,当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2时,则$\frac{3}{a}$+$\frac{2}{b}$的最小值为( )
| A. | $\frac{25}{6}$ | B. | 4$+\sqrt{3}$ | C. | 4$+2\sqrt{3}$ | D. | 4$\sqrt{3}$ |
4.某商品价格先涨10%.再降10%出售,则最终价格与原价相比( )
| A. | 上涨了 | B. | 下降了 | C. | 相等 | D. | 是否上涨不一定 |
11.设函数f(x)=$\frac{1}{2}$x2-3x+31nx+3,则下列区间中有零点的是( )
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,2) | D. | (2,e) |
8.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(1,1),若($\overrightarrow{a}$+$λ\overrightarrow{b}$)⊥$\overrightarrow{b}$,则λ等于( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
9.在等比数列{an}中,a5+a6=2,a15+a16=3,则a25+a26的值是( )
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{9}{2}$ | D. | $\frac{3}{4}$ |
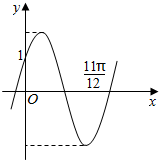 函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示
函数f(x)=2sin(ωx+φ)(ω>0)的图象如图所示