题目内容
5．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4x，x≥0}\\{\frac{x}{x-1}，x＜0}\end{array}\right.$，则不等式f（x）＞x的解集为（-∞，0）∪（5，+∞）．分析 分类讨论，从而化为x2-4x＞x或$\frac{x}{x-1}$＞x，从而解得．
解答 解：①当x≥0时，f（x）＞x可化为x2-4x＞x，
解得，x＞5；
②当x＜0时，f（x）＞x可化为$\frac{x}{x-1}$＞x，
解得，x＜0；
故答案为：（-∞，0）∪（5，+∞）．
点评 本题考查了分段函数的应用及分类讨论的思想应用．
练习册系列答案
相关题目
15．设函数f（x）在点x0可导，且$\underset{lim}{h→0}$$\frac{f（{x}_{0}）-f（{x}_{0}-2h）}{h}$=3，则f′（x0）=（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | -$\frac{3}{2}$ | D． | 3 |
13．
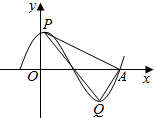函数y=$\sqrt{3}$sin（ωx+φ）（ω＞0，φ＞0）的部分图象如图所示，设P，Q分别是图象的相邻的最高点和最低点，A是图象与x轴的交点，若AP⊥AQ，则ω的值为（ ）
函数y=$\sqrt{3}$sin（ωx+φ）（ω＞0，φ＞0）的部分图象如图所示，设P，Q分别是图象的相邻的最高点和最低点，A是图象与x轴的交点，若AP⊥AQ，则ω的值为（ ）| A． | π | B． | $\frac{π}{2}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{4}$ |
10．已知a+a-1=2，则a-a-1的值为（ ）
| A． | 0 | B． | 2 | C． | -2 | D． | $\sqrt{2}$ |
14．设a、b、c均为正实数，且3a=4b=6c，那么（ ）
| A． | $\frac{2}{c}=\frac{2}{a}+\frac{1}{b}$ | B． | $\frac{1}{c}=\frac{2}{a}+\frac{2}{b}$ | C． | $\frac{1}{c}=\frac{1}{a}+\frac{1}{b}$ | D． | $\frac{2}{c}=\frac{1}{a}+\frac{2}{b}$ |
