题目内容
15.设函数f(x)在点x0可导,且$\underset{lim}{h→0}$$\frac{f({x}_{0})-f({x}_{0}-2h)}{h}$=3,则f′(x0)=( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | 3 |
分析 根据导数的极限定义进行转化求解即可.
解答 解:∵函数f(x)在点x0可导,且$\underset{lim}{h→0}$$\frac{f({x}_{0})-f({x}_{0}-2h)}{h}$=3,
∴$\underset{lim}{h→0}$$\frac{f({x}_{0})-f({x}_{0}-2h)}{h}$=$\underset{lim}{h→0}$$\frac{f({x}_{0}-2h)-f({x}_{0})}{-h}$=2$\underset{lim}{h→0}$$\frac{f({x}_{0}-2h)-f({x}_{0})}{-2h}$=2f′(x0)=3,
则f′(x0)=$\frac{3}{2}$,
故选:A
点评 本题主要考查导数的概念,利用导数的几何意义,转化为极限形式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.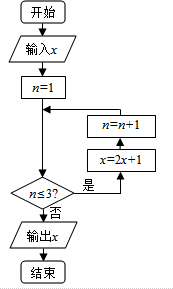 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |