题目内容
16.设函数f(x)=ex(x3-3x+3)-aex-x,e为自然对数的底数,若不等式f(x)≤0在x∈[-2,+∞)有解,则实数a的最小值为1-$\frac{1}{e}$.分析 化简可得a≥x3-3x+3-$\frac{x}{{e}^{x}}$,令g(x)=x3-3x+3-$\frac{x}{{e}^{x}}$,从而求导g′(x)=3x2-3+$\frac{x-1}{{e}^{x}}$=(x-1)(3x+3+$\frac{1}{{e}^{x}}$),从而确定gmin(x)=g(1)=1-3+3-$\frac{1}{e}$=1-$\frac{1}{e}$;从而解得.
解答 解:∵f(x)=ex(x3-3x+3)-aex-x≤0,
∴a≥x3-3x+3-$\frac{x}{{e}^{x}}$,
令g(x)=x3-3x+3-$\frac{x}{{e}^{x}}$,
g′(x)=3x2-3+$\frac{x-1}{{e}^{x}}$
=(x-1)(3x+3+$\frac{1}{{e}^{x}}$),
故当x∈[-2,1)时,g′(x)<0,
当x∈(1,+∞)时,g′(x)>0,
故g(x)在[-2,1)上是减函数,在(1,+∞)上是增函数;
故gmin(x)=g(1)=1-3+3-$\frac{1}{e}$=1-$\frac{1}{e}$;
故答案为:1-$\frac{1}{e}$.
点评 本题考查了不等式的化简与应用,同时考查了导数的综合应用及存在性问题的应用.

练习册系列答案
相关题目
6.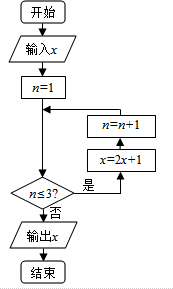 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
 在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )
在闭区间[-4,6]上随机取出-个数x,执行如右图所示的程序框图,则输出的x不小于39的概率为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
8.A,B,C是不共线的三点,对空间任意一点O,有$\overrightarrow{OD}$=$\frac{1}{3}$($\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$).则D点( )
| A. | 不在平面ABC内 | B. | D是△ABC的重心 | C. | D是△ABC的外心 | D. | D是△ABC的垂心 |