Question

13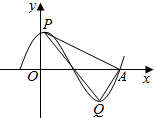．函数y=$\sqrt{3}$sin（ωx+φ）（ω＞0，φ＞0）的部分图象如图所示，设P，Q分别是图象的相邻的最高点和最低点，A是图象与x轴的交点，若AP⊥AQ，则ω的值为（　　）

• A． π
• B． $\frac{π}{2}$
• C． $\frac{π}{3}$
• D． $\frac{π}{4}$

Answer 1

分析 设P、Q、A的坐标分别为（x₁，$\sqrt{3}$）、（x₂，-$\sqrt{3}$）、（x₃，0），可得x₃-x₁=$\frac{3π}{2ω}$，x₃-x₂=$\frac{π}{2ω}$．再利用$\overrightarrow{AP}$•$\overrightarrow{AQ}$=0，求得ω的值．

解答 解：设P、Q、A的坐标分别为（x₁，$\sqrt{3}$）、（x₂，-$\sqrt{3}$）、（x₃，0），
则ωx₁+φ=$\frac{π}{2}$，ωx₂+φ=$\frac{3π}{2}$，ωx₃+φ=2π，x₃-x₁=$\frac{3π}{2ω}$，x₃-x₂=$\frac{π}{2ω}$．
由AP⊥AQ，可得$\overrightarrow{AP}$•$\overrightarrow{AQ}$=（x₁-X₃，$\sqrt{3}$）•（x₂-x₃，-$\sqrt{3}$）=（-$\frac{3π}{2ω}$，$\sqrt{3}$）•（-$\frac{π}{2ω}$，-$\sqrt{3}$）=$\frac{{3π}^{2}}{{4ω}^{2}}$-3=0，
求得ω=$\frac{π}{2}$，
故选：B．

点评 本题主要考查正弦函数的图象的特征，两个向量的数量积的运算，属于中档题．