若a＞b＞0.则直线$y=\frac{b}{a}x+b$与椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$在同一坐标系中的位置只可能是( )A．B．C．D．题目和参考答案——青夏教育精英家教网——

题目内容

19．若a＞b＞0，则直线$y=\frac{b}{a}x+b$与椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$在同一坐标系中的位置只可能是（　　）

A．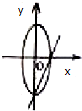

B．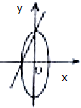

C．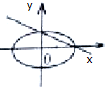

D．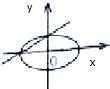

分析利用a＞b＞0，推出直线的斜率，在y轴上的截距，椭圆的焦点坐标的位置，即可判断图形．

解答解：a＞b＞0，可知直线的斜率大于0，在y轴上的截距为正，椭圆的焦点坐标在x轴上，
故选：D．

点评本题考查椭圆的简单性质与直线的位置的判断，是基础题．

练习册系列答案

蓉城学堂中考总复习点击与突破系列答案

中考导航模拟卷系列答案

本土教辅名校作业系列答案

常青藤英语完形填空与阅读理解系列答案

蓝卡中考试题解读系列答案

中考新动向系列答案

一考通综合训练系列答案

新课程指导与练习系列答案

中考阶段总复习模拟试题系列答案

全程助学与学习评估系列答案

相关题目

5．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-4x，x≥0}\\{\frac{x}{x-1}，x＜0}\end{array}\right.$，则不等式f（x）＞x的解集为（-∞，0）∪（5，+∞）．

10．集合A={x|$\frac{x+3}{2-x}$≥1}，函数f（x）=log${\;}_{\frac{1}{2}}$$\frac{x-{a}^{2}-1}{x-a}$的定义域为集合B．
（1）求集合A和B；
（2）若A?B，求实数a的取值范围．

7．已知tan（π+x）=2
（1）求$\frac{2sinx-3cosx}{sinx+5cosx}$的值；
（2）求$\frac{1}{{2{{sin}^2}x-sinxcosx+{{cos}^2}x}}$的值．

14．某人年初用98万元购买了一条渔船，第一年各种费用支出为12万元，以后每年都增加4万元，而每年捕鱼收益为50万元．第几年他开始获利？（　　）

4．函数 f（x）=sin（x+φ）-2sinφcosx的值域是[-1，1]．

11．已知函数f（2x-1）=3x+2，则f（5）=11．

8．若圆C的半径为1，圆心C与点（2，0）关于直线x+y-1=0对称，则圆C的标准方程为（　　）

（x-1）²+（y+1）²=1

（x-1）²+（y-1）²=1

（x+1）²+（y+1）²=1

（x+1）²+（y-1）²=1

9．已知集合A=$\{x|y=\sqrt{{x^2}-x-6}\}$，集合B=$\{x|x=lo{g_{\frac{1}{2}}}a，a＞1\}$，则（∁_RA）∩B=（　　）