题目内容
 如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,点P为面ADD1A1的对角线AD1上的动点(不包括端点).PM⊥平面ABCD交AD于点M,MN⊥BD于点N.
如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,点P为面ADD1A1的对角线AD1上的动点(不包括端点).PM⊥平面ABCD交AD于点M,MN⊥BD于点N.(1)设AP=x,将PN长表示为x的函数;
(2)当PN最小时,求异面直线PN与A1C1所成角的大小.(结果用反三角函数值表示)
考点:异面直线及其所成的角,函数解析式的求解及常用方法
专题:计算题,函数的性质及应用,空间角
分析:(1)求出PM,AM,运用余弦定理,求得PN;
(2)求出PN的最小值,由于MN∥AC,又A1C1∥AC,∠PNM为异面直线PN与A1C1所成角的平面角,通过解直角三角形PMN,即可得到.
(2)求出PN的最小值,由于MN∥AC,又A1C1∥AC,∠PNM为异面直线PN与A1C1所成角的平面角,通过解直角三角形PMN,即可得到.
解答:
解:(1)在△APM中,PM=
,AM=
;
其中0<x<2
;
在△MND中,MN=
(2-
x),
在△PMN中,PN=
,x∈(0,2
);
(2)当x=
∈(0,2
)时,PN最小,此时PN=
.
因为在底面ABCD中,MN⊥BD,AC⊥BD,所以MN∥AC,又A1C1∥AC,
∠PNM为异面直线PN与A1C1所成角的平面角,
在△PMN中,∠PMN为直角,tan∠PNM=
,
所以∠PNM=arctan
,
异面直线PN与A1C1所成角的大小arctan
.
2
| ||
| 5 |
| ||
| 5 |
其中0<x<2
| 5 |
在△MND中,MN=
| ||
| 2 |
| ||
| 5 |
在△PMN中,PN=
|
| 5 |
(2)当x=
2
| ||
| 9 |
| 5 |
| 4 |
| 3 |
因为在底面ABCD中,MN⊥BD,AC⊥BD,所以MN∥AC,又A1C1∥AC,
∠PNM为异面直线PN与A1C1所成角的平面角,
在△PMN中,∠PMN为直角,tan∠PNM=
| ||
| 4 |
所以∠PNM=arctan
| ||
| 4 |
异面直线PN与A1C1所成角的大小arctan
| ||
| 4 |
点评:本题考查空间异面直线所成的角的求法,考查二次函数的性质和运用:求最值,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)=
(a>0a≠1),其中[m]表示不超过m的最大整数,如[4.1]=4,则函数y=[f(x)-
]+[f(-x)-
]的值域是( )
| ax |
| 1+ax |
| 1 |
| 2 |
| 1 |
| 2 |
| A、{0,1} |
| B、{-1,1} |
| C、{-1,0} |
| D、{-1,0,1} |
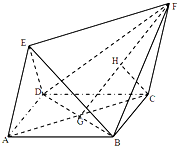 如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=
如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=