题目内容
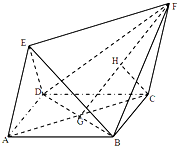 如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=
如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=| 3 |
(Ⅰ)证明:CH⊥面BFD;
(Ⅱ)若CH=
| ||
| 2 |
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)首先根据已知条件利用菱形的性质求出垂直的关系,进一步利用面面垂直得到线线垂直,最后利用线面垂直的判定求出结论.
(Ⅱ)利用上步的结论,先确定线面的夹角,进一步求出角的大小.
(Ⅱ)利用上步的结论,先确定线面的夹角,进一步求出角的大小.
解答:
(Ⅰ)证明:四边形ABCD为菱形
所以:BD⊥AC
又面ACEF⊥面ABCD
所以:BD⊥平面ACFE
所以:BD⊥CH
即:CH⊥BD
又H为FG的中点,CG=CF=
所以:CH⊥FG
所以:CH⊥面BFD.
(Ⅱ)连接EG,由(Ⅰ)知BD⊥平面ACFE
所以:面EFG⊥面BED
所以:EF与平面EDB所成的角即为∠FEG.
在△FCG中,CG=CF=
,CH=
,CH⊥GF
所以∠GCF=120°,GF=3
所以EG=
,又因为EF=2
.
所以在△EFG中,可求得∠FEG=60°

所以:BD⊥AC
又面ACEF⊥面ABCD
所以:BD⊥平面ACFE
所以:BD⊥CH
即:CH⊥BD
又H为FG的中点,CG=CF=
| 3 |
所以:CH⊥FG
所以:CH⊥面BFD.
(Ⅱ)连接EG,由(Ⅰ)知BD⊥平面ACFE
所以:面EFG⊥面BED
所以:EF与平面EDB所成的角即为∠FEG.
在△FCG中,CG=CF=
| 3 |
| ||
| 2 |
所以∠GCF=120°,GF=3
所以EG=
| 3 |
| 3 |
所以在△EFG中,可求得∠FEG=60°

点评:本题考查的知识要点:线面垂直的判定,线面的夹角的应用.属于基础题型.

练习册系列答案
相关题目
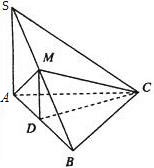 如图所示,三棱锥S-ABC中,SA⊥AC,AC⊥BC,M为SB的中点,D为AB的中点,且△AMB为正三角形.
如图所示,三棱锥S-ABC中,SA⊥AC,AC⊥BC,M为SB的中点,D为AB的中点,且△AMB为正三角形. 如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,点P为面ADD1A1的对角线AD1上的动点(不包括端点).PM⊥平面ABCD交AD于点M,MN⊥BD于点N.
如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,点P为面ADD1A1的对角线AD1上的动点(不包括端点).PM⊥平面ABCD交AD于点M,MN⊥BD于点N.