题目内容
若N（x）=（1+x）2-1+ln（1+x），判断并证明N（x）在（-1，+∞）上的单调性．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：直接由函数的导函数的符号判断原函数的单调性．
解答：
解：函数N（x）=（1+x）2-1+ln（1+x）在（-1，+∞）上单调递增．
证明如下：由N（x）=（1+x）2-1+ln（1+x），得
N′(x)=2(1+x)+
=
，
当x＞-1时，N′（x）＞0，
∴N（x）在（-1，+∞）上单调递增．
证明如下：由N（x）=（1+x）2-1+ln（1+x），得
N′(x)=2(1+x)+
| 1 |
| 1+x |
| 2(1+x)2+1 |
| 1+x |
当x＞-1时，N′（x）＞0，
∴N（x）在（-1，+∞）上单调递增．
点评：本题考查了利用导数研究函数的单调性，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减，是基础题．
练习册系列答案
相关题目
如图，长方体ABCD-A1B1C1D1中，AB=AD=2，AA1=4，点P为面ADD1A1的对角线AD1上的动点（不包括端点）．PM⊥平面ABCD交AD于点M，MN⊥BD于点N．已知a，b∈[-2，2]，在此范围内任取数对（a，b），能使函数f（x）=x3-3x+a+b，有三个不同零点的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
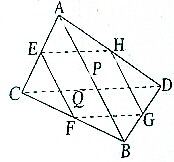如图所示，线段AB、CD所在直线是异面直线，E、F、G、H分别是线段AC、CB、BD、DA的中点．