题目内容
函数f（x）=2x2-4x-3的零点个数为 ．
考点：函数零点的判定定理
专题：函数的性质及应用
分析：要求函数的零点，即为研究方程的根，因此只需用判别式判断该二次方程的根的个数即可．
解答：
解：函数f（x）=2x2-4x-3的零点即为2x2-4x-3=0的根，
因为△=（-4）2+4×3×2=40＞0．
所以该二次方程有两个不相等的实数根，
所以函数f（x）=2x2-4x-3有2个零点．
故答案为2
因为△=（-4）2+4×3×2=40＞0．
所以该二次方程有两个不相等的实数根，
所以函数f（x）=2x2-4x-3有2个零点．
故答案为2
点评：本题考查了函数的零点与方程的根之间的关系，一般的它们之间是可以相互转化的．可以互为方法利用的．
练习册系列答案
同步练习强化拓展系列答案
相关题目
设集合A={x|-1＜x＜2}，集合B={x|1＜x＜3}，则A∪B等于（ ）
| A、{ x|2＜x＜3} |
| B、{x|-1＜x＜3} |
| C、{x|-1＜x＜2} |
| D、{x|-1＜x＜1} |
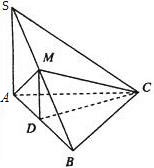如图所示，三棱锥S-ABC中，SA⊥AC，AC⊥BC，M为SB的中点，D为AB的中点，且△AMB为正三角形．
如图，长方体ABCD-A1B1C1D1中，AB=AD=2，AA1=4，点P为面ADD1A1的对角线AD1上的动点（不包括端点）．PM⊥平面ABCD交AD于点M，MN⊥BD于点N．