题目内容
方
+
=-1的曲线即为函y=f(x)的图象,对于函数y=f(x),有如下结论:
①x在R上单调递减;
②函数F(x)=4f(x)+3x不存在零点;
③函数y=f(x)的值域是R;
④若函数g(x)和f(x)的图象关于原点对称,则函数y=g(x)的图象就是方程
+
=1确定的曲线.
其中所有正确的命题序号是 .
| x|x| |
| 16 |
| y|y| |
| 9 |
①x在R上单调递减;
②函数F(x)=4f(x)+3x不存在零点;
③函数y=f(x)的值域是R;
④若函数g(x)和f(x)的图象关于原点对称,则函数y=g(x)的图象就是方程
| y|y| |
| 16 |
| x|x| |
| 9 |
其中所有正确的命题序号是
考点:圆锥曲线的共同特征
专题:函数的性质及应用,圆锥曲线的定义、性质与方程
分析:根据题意,化简方程方
+
=-1,作出函数y=f(x)的图象,
由函数的图象判断函数在R上的单调性以及值域,得出①③是否正确;
判断F(x)=4f(x)+3x=0是否存在零点,得出②是否正确;
根据函数的对称性得出g(x)的解析式是什么,判断④是否正确.
| x|x| |
| 16 |
| y|y| |
| 9 |
由函数的图象判断函数在R上的单调性以及值域,得出①③是否正确;
判断F(x)=4f(x)+3x=0是否存在零点,得出②是否正确;
根据函数的对称性得出g(x)的解析式是什么,判断④是否正确.
解答:
解:对于①,根据题意画出方程
+
=-1的曲线,即为函数y=f(x)的图象,如图所示;
轨迹是两段双曲线的一部分加上一段的椭圆圆弧组成的图形.
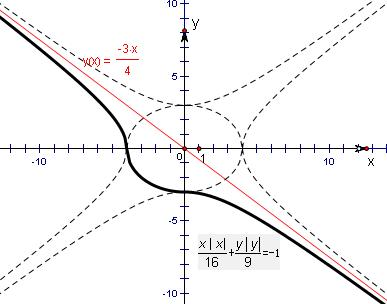
从图形中可以看出,关于函数y=f(x)的有下列说法:
①f(x)在R上单调递减,∴①正确;
②由于4f(x)+3x=0即f(x)=-
x,从而图形上看,函数f(x)的图象与直线y=-
x没有交点,
∴函数F(x)=4f(x)+3x不存在零点,②正确;
③函数y=f(x)的值域是R,∴③正确;
④若函数g(x)和f(x)的图象关于原点对称,
则函数y=g(x)的图象是方程
+
=1确定的曲线,∴④错误.
综上,以上正确的命题是①②③.
故答案为:①②③.
| x|x| |
| 16 |
| y|y| |
| 9 |
轨迹是两段双曲线的一部分加上一段的椭圆圆弧组成的图形.

从图形中可以看出,关于函数y=f(x)的有下列说法:
①f(x)在R上单调递减,∴①正确;
②由于4f(x)+3x=0即f(x)=-
| 3 |
| 4 |
| 3 |
| 4 |
∴函数F(x)=4f(x)+3x不存在零点,②正确;
③函数y=f(x)的值域是R,∴③正确;
④若函数g(x)和f(x)的图象关于原点对称,
则函数y=g(x)的图象是方程
| x|x| |
| 16 |
| y|y| |
| 9 |
综上,以上正确的命题是①②③.
故答案为:①②③.
点评:本题考查了含有绝对值的二次方程的曲线问题,也考查了含有绝对值的函数式的化简、函数的图象与性质、直线与圆锥曲线的位置关系等知识的应用问题,解题的关键是画出函数的图象,是难题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
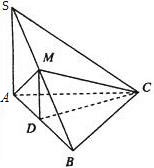 如图所示,三棱锥S-ABC中,SA⊥AC,AC⊥BC,M为SB的中点,D为AB的中点,且△AMB为正三角形.
如图所示,三棱锥S-ABC中,SA⊥AC,AC⊥BC,M为SB的中点,D为AB的中点,且△AMB为正三角形. 如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,点P为面ADD1A1的对角线AD1上的动点(不包括端点).PM⊥平面ABCD交AD于点M,MN⊥BD于点N.
如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4,点P为面ADD1A1的对角线AD1上的动点(不包括端点).PM⊥平面ABCD交AD于点M,MN⊥BD于点N.