题目内容

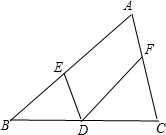
在△ABC中，E，F分别在边AB，AC上，D为BC的中点，满足
|
AE
|
|
EB
|
=
|
CF
|
|
FA
|
=
|
AB
|
|
AC
|
=2，
DE
•
DF
=0，则 cos A=（　　）
A、0
B、
3
2
C、
3
4
D、
9
16
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据共线向量基本定理及已知的边的关系即可用向量
AB
，
AC
表示
DE
，
DF
：
DE
=
1
6
AB
-
1
2
AC
，
DF
=-
1
2
AB
-
1
6
AC
，根据
DE
•
DF
=0，及|
AB
|=2|
AC
|即可求出cosA．
解答： 解：如图，根据已知条件得：
DE
=
DB
+
BE
=
1
2
CB
+
1
3
BA
=
1
2
(
AB
-
AC
)-
1
3
AB
=
1
6
AB
-
1
2
AC
；
DF
=
DC
+
CF
=
1
2
BC
+
2
3
CA
=
1
2
(
AC
-
AB
)-
2
3
AC
=-
1
2
AB
-
1
6
AC
；
∴
DE
•
DF
=(
1
6
AB
-
1
2
AC
)•(-
1
2
AB
-
1
6
AC
)=-
1
12
AB
2+
2
9
AB
•
AC
+
1
12
AC
2=0；
把|
AB
|=2|
AC
|带入上式并整理得：cosA=
9
16
．
故选：D．
点评：考查共线向量基本定理，向量的加法运算，向量的减法运算，向量的数量积的运算及运算公式．
练习册系列答案
相关题目
已知集合A=（-5，1），B=（-∞，a），若A∩B=∅，则实数a的取值范围是
 
．
设集合M={y|y=x2-1，x∈R}，N={y|2x2-4x+1，x∈R}，则集合M与N的关系为（　　）
A、M∩N=MB、M∪N=M
C、M=ND、M∩N=∅
设点P是椭圆
x2
25
+
y2
9
=1上的动点，F1、F2是椭圆上的两个焦点，求sin∠F1PF2的最大值．
已知函数f（x）=ax3-3x2+1，若f（x）存在唯一的零点x°，且x°＜0，则a的取值范围是
 
．
已知函数f（x）与g（x）在R上有定义，f（x-y）=f（x）g（y）-g（x）f（y）对任意的实数x，y都成立，且f（1）=f（2）≠0，则g（1）+g（-1）=
 
．
已知数列{an}满足an=1，
1，n=1
kan-1+2，n＞1
，则
（1）当k=1时，求数列{an}的前n项和sn；
（2）当k=2时，证明数列{an+2}是等比数列．
有一长为24米的篱笆，一面利用墙（墙最大长度是 10米）围成一个矩形花圃，设该花圃宽AB为x米，面积是y平方米，
（1）求出y关于x的函数解析式，并指出x的取值范围；
（2）当花圃一边AB为多少米时，花圃面积最大？并求出这个最大面积？
某单位在国庆节7天假期里安排甲、乙、丙三人值班，每天1人，每人至少值2天，则不同的安排方法共有
 
种．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网