题目内容
2.已知对数函数 f(x)=logax(a>0,且a≠1)在区间[2,4]上的最大值与最小值之积为2,则a=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$或 2 | C. | $2\sqrt{2}$ | D. | 2 |
分析 当0<a<1时,loga2•loga4=2(loga2)2=2,当a>1时,loga2•loga4=2(loga2)2=2,由此能求出a的值.
解答 解:∵对数函数 f(x)=logax(a>0,且a≠1)在区间[2,4]上的最大值与最小值之积为2,
∴①当0<a<1时,loga2•loga4=2(loga2)2=2,
∴loga2=±1,
当loga2=1时,a=2,(舍);当loga2=-1时,a=$\frac{1}{2}$.
②当a>1时,loga2•loga4=2(loga2)2=2,
∴loga2=±1,
当loga2=1时,a=2;当loga2=-1时,a=$\frac{1}{2}$.(舍)
综上,a的值为$\frac{1}{2}$或2.
故选:B.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意对数函数性质的合理运用.

练习册系列答案
相关题目
20.设p:x<2,q:-2<x<2,则p是q成立的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.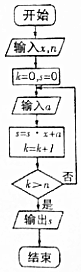 如图是实现秦九韶算法的程序框图,若输入的x=2,n=2,依次输入a=3,4,5,6,7,…,则输出的s=( )
如图是实现秦九韶算法的程序框图,若输入的x=2,n=2,依次输入a=3,4,5,6,7,…,则输出的s=( )
 如图是实现秦九韶算法的程序框图,若输入的x=2,n=2,依次输入a=3,4,5,6,7,…,则输出的s=( )
如图是实现秦九韶算法的程序框图,若输入的x=2,n=2,依次输入a=3,4,5,6,7,…,则输出的s=( )| A. | 3 | B. | 10 | C. | 25 | D. | 56 |
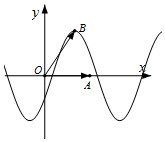 直角坐标系xOy中,已知点A(1,0),函数f(x)=sin(2x-$\frac{π}{6}$)的图象在y轴右侧的第一个最高点为B,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{π}{3}$.
直角坐标系xOy中,已知点A(1,0),函数f(x)=sin(2x-$\frac{π}{6}$)的图象在y轴右侧的第一个最高点为B,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{π}{3}$.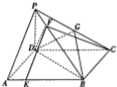 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PA⊥PC,∠ADC=120°,底面ABCD为菱形,G为PC中点,E,F分别为AB,PB上一点,AB=4AE=4$\sqrt{2}$,PB=4PF.