题目内容
11．设曲线y=x2-x在点（3，6）处的切线与直线ax+y+1=0垂直，则a=$\frac{1}{5}$．分析 求函数的导数，得到切线斜率，根据直线垂直关系即可得到解得结论．
解答 解：函数的导数y′=2x-1，
则曲线y=x2-x在点（3，6）处的切线斜率k=5，
∵直线ax+y+1=0的斜截式方程为y=-ax-1，斜率为-a，
∴若切线与直线ax+y+1=0垂直，则-a×5=-1，
则a=$\frac{1}{5}$，
故答案为$\frac{1}{5}$．
点评 本题主要考查直线垂直的关系的应用以及利用导数求切线斜率，利用导数的几何意义是解决本题的关键．
练习册系列答案
相关题目
9．函数f（x）=sin（2x+$\frac{π}{3}$）（ ）
| A． | 图象向右平移$\frac{π}{3}$个单位长度得到y=sin2x图象 | |
| B． | 图象关于点（$\frac{π}{6}$，0）对称 | |
| C． | 图象关于直线x=-$\frac{π}{12}$对称 | |
| D． | 在区间[-$\frac{5π}{12}$，$\frac{π}{12}$]单调递增 |
2．已知对数函数 f（x）=logax（a＞0，且a≠1）在区间[2，4]上的最大值与最小值之积为2，则a=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{2}$或 2 | C． | $2\sqrt{2}$ | D． | 2 |
19．函数f（x）是定义在（-∞，0）上的可导函数，其导函数为f′（x），且有3xf（x）+x2f（x）＜0，则不等式（x+2016）3f（x+2016）+27f（-3）＞0的解集（ ）
| A． | （-2018，-2016） | B． | （-∞，-2016） | C． | （-2019，-2016） | D． | （-∞，-2019） |
6．
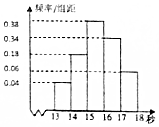为调查运城市学生百米运动成绩，从该市学生中按照男女比例随机抽取50名学生进行百米测试，学生成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
（Ⅰ）求这组数据的中位数（精确到0.1）
（Ⅱ）根据有关规定，成绩小于16秒为达标．如果男女生使用相同的达标标准，则男女生达标情况如表：
根据表中所给的数据，能否有99%的把握认为“体育达标与性别有关”？若有，你能否提出一个更好的解决方法来？
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
为调查运城市学生百米运动成绩，从该市学生中按照男女比例随机抽取50名学生进行百米测试，学生成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．（Ⅰ）求这组数据的中位数（精确到0.1）
（Ⅱ）根据有关规定，成绩小于16秒为达标．如果男女生使用相同的达标标准，则男女生达标情况如表：
| 性别 是否达标 | 男 | 女 | 合计 |
| 达标 | a=24 | b=6 | 30 |
| 不达标 | c=8 | d=12 | 20 |
| 合计 | 32 | 18 |
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥K） | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.625 | 10.828 |
16．
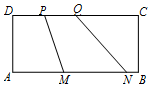如图，矩形ABCD中，AB=2AD=4，MN=2PQ=2，向该矩形内随机投一质点，则质点落在四边形MNQP内的概率为（ ）
如图，矩形ABCD中，AB=2AD=4，MN=2PQ=2，向该矩形内随机投一质点，则质点落在四边形MNQP内的概率为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{3}{8}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
3．
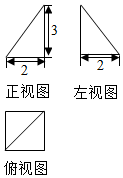已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）
已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）| A． | $\frac{4}{3}$cm3 | B． | $\frac{8}{3}$cm3 | C． | 2cm3 | D． | 4cm3 |
20．等差败列{an}的前n项和为Sn，若a3+a16=10，则S18=（ ）
| A． | 50 | B． | 90 | C． | 100 | D． | 190 |