题目内容
20.设p:x<2,q:-2<x<2,则p是q成立的( )| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义进行判断即可.
解答 解:当x=-3时,满足x<2,但-2<x<2不成立,
若-2<x<2,则x<2成立,即p是q成立的必要不充分条件,
故选:B
点评 本题主要考查充分条件和必要条件的判断,根据不等式的关系是解决本题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
10.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如表):
由最小二乘法求得回归方程 $\widehat{y}$=0.67x+a,则a的值为54.9.
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 68 | 75 | 81 | 89 |
11.某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )
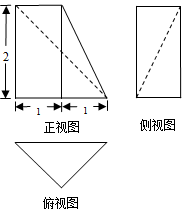

| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\sqrt{2}$ |
15.已知$sin(α+\frac{π}{6})=\frac{1}{3}$,则$cos(2α-\frac{2π}{3})$的值是( )
| A. | $\frac{5}{9}$ | B. | $-\frac{8}{9}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{7}{9}$ |
5.某四棱锥的三视图如图所示,该四棱锥的表面积是( )


| A. | 32 | B. | 16+16$\sqrt{2}$ | C. | 48 | D. | 16+32$\sqrt{2}$ |
12.命题“$?{x_0}∈R,{2^{x_0}}≤0$”的否定是( )
| A. | 不存在${x_0}∈R,{2^{x_0}}>0$ | B. | ?x∈R,2x>0 | ||
| C. | $?{x_0}∈R,{2^{x_0}}≥0$. | D. | ?x∈R,2x≤0 |
9.函数f(x)=sin(2x+$\frac{π}{3}$)( )
| A. | 图象向右平移$\frac{π}{3}$个单位长度得到y=sin2x图象 | |
| B. | 图象关于点($\frac{π}{6}$,0)对称 | |
| C. | 图象关于直线x=-$\frac{π}{12}$对称 | |
| D. | 在区间[-$\frac{5π}{12}$,$\frac{π}{12}$]单调递增 |
2.已知对数函数 f(x)=logax(a>0,且a≠1)在区间[2,4]上的最大值与最小值之积为2,则a=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$或 2 | C. | $2\sqrt{2}$ | D. | 2 |